Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: N∈BC
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có
M∈AB(gt)
N∈BC(gt)
MN//BC(gt)
Do đó: \(\dfrac{NC}{BC}=\dfrac{AM}{AB}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{NC}{10}=\dfrac{4}{6}=\dfrac{2}{3}\)
hay \(NC=\dfrac{20}{3}cm\)
Ta có: NC+NB=BC(N nằm giữa B và C)
hay \(NB=BC-NC=10-\dfrac{20}{3}=\dfrac{10}{3}cm\)
Xét ΔABC có
N∈BC(gt)
M∈AB(gt)
MN//AC(gt)
Do đó: \(\dfrac{MN}{AC}=\dfrac{BN}{BC}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow\dfrac{MN}{8}=\dfrac{10}{3}:10\)
\(\Leftrightarrow MN=\dfrac{10}{3}\cdot\dfrac{1}{10}\cdot8\)
hay \(MN=\dfrac{8}{3}cm\)
Vậy: \(NC=\dfrac{20}{3}cm\); \(MN=\dfrac{8}{3}cm\)

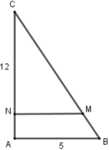
Tam giác ABC vuông tại A, theo định lí Pi-ta-go ta có:
B C 2 = A B 2 + A C 2 ⇒ B C 2 = 5 2 + 12 2 = 169 ⇒ B C = 13
BM = 5 13 BC = 5 13 .13 = 5 => CM = 13 - 5 = 8.
Xét ΔCMN và ΔCBA có:
N = A = 90 ∘ (gt)
Góc C chung
=> ΔCMN ~ ΔCBA (g - g) => (cạnh tương ứng)
⇒ M N = A B . C M C B = 5.8 13 = 40 13
Đáp án: C

Đề bài của bn bị thiếu à?
Cho tam giác ABC vuông tai A (AB ?

:V chụp xong không gửi được cái phần kia nên mình chép ra vậy hình bạn tự vẽ nhé v
a) Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A ta được:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
Xét tam giác ABC có MN//BC (gt)
\(\Rightarrow\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}\)( hệ quả của định lý Ta-let)
\(\Rightarrow\frac{3}{4}=\frac{AN}{8}=\frac{MN}{10}\)
\(\Rightarrow\hept{\begin{cases}AN=6\left(cm\right)\\MN=7,5\left(cm\right)\end{cases}}\)
b)Vì MI//AC (gt)
\(\Rightarrow MI//AK\left(K\in AB\right)\)
Vì IK//AB(gt)
\(\Rightarrow IK//AM\left(M\in AB\right)\)
Ta có: \(\hept{\begin{cases}MI//AK\left(cmt\right)\\IK//AM\left(cmt\right)\end{cases}\Rightarrow MI=AK}\)( tc cặp đoạn chắn)
Ta có: AM+MB=AB
\(\Rightarrow MB=1,5\left(cm\right)\)
Xét tam giác ABC có MI//AB(gt)

Cho biểu thức B=\(\frac{2x+1}{x^2-1}\); A= \(\frac{3x+1}{x^2-1}\)--\(\frac{x}{x-1}\)+\(\frac{x-1}{x+1}\) (x khác +,- 1; x khác \(\frac{-1}{2}\))
a) Tính giá trị của B biết x=-2
b) Rút gọn A
c) Cho P=A:B Tìm x biết P=3
Cho biểu thức A=\(\left(\frac{2x-3}{x^2-9}-\frac{2}{x+3}\right):\frac{x}{x+3}\)(x khác +,- 3)
a) Rút gọn A
b) TÍnh giá trị của A khi x=\(-\frac{1}{2}\)
c) Tìm các giá trị nguyên của x để A nhận giá trị nguyên

Bài 1:

Áp dụng tính chất đường phân giác của tam giác ta có:
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{18}=\frac{2}{3}\)
\(\Rightarrow\frac{BD}{2}=\frac{DC}{3}=\frac{BD+DC}{2+3}=\frac{BC}{5}\Rightarrow\frac{BD}{BC}=\frac{2}{5}\)
Kẻ \(DK//BE\left(K\in AC\right)\text{ ta có:}\)
\(\frac{AE}{EK}=\frac{AI}{ID}=2;\frac{EK}{EC}=\frac{BD}{BC}=\frac{2}{5}\)
Do đó:\(\frac{AE}{EK}\cdot\frac{EK}{EC}=\frac{AE}{EC}=\frac{2}{5}.2=\frac{4}{5}\)
b)\(\text{Ta có:}\)
\(\frac{AE}{EC}=\frac{4}{5}\Rightarrow\frac{AE}{4}=\frac{EC}{5}=\frac{AE+EC}{4+5}=\frac{AC}{9}=\frac{18}{9}=2\)
\(\Rightarrow AE=8cm,EC=10cm\)
bn ơi bài 1 ý a) chỉ có thể tính tỉ lệ thôi ko tính đc ra số hẳn đâu

a: Xét tứ giác ANMP có
\(\widehat{ANM}=\widehat{APM}=\widehat{NAP}=90^0\)
=>ANMP là hình chữ nhật
c: Xét ΔABC có
M là trung điểm của BC
MN//AC
Do đó: N là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MP//AB
Do đó: P là trung điểm của AC
Xét ΔABC có
N,P lần lượt là trung điểm của AB,AC
=>NP là đường trung bình của ΔABC
=>NP//BC và NP=BC/2
=>NP//MH
Ta có: ΔHAC vuông tại H
mà HP là đường trung tuyến
nên HP=AP
mà AP=MN(ANMP là hình chữ nhật)
nên HP=MN
Xét tứ giác MHNP có MH//NP
nên MHNP là hình thang
Hình thang MHNP có MN=HP
nên MHNP là hình thang cân
BM=AB-AM=12-3=9
ta có
BA vuông góc AC
BA vuông góc MN
=>AC//MN
áp dụng hệ quả của te-lét ta đc
BM/BA=MN/AC
=>9/12=15/AC
=>15.12/9=AC
=>AC=180/9=20