Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) AC = 10cm Þ SABC =37,5 (cm2)
b) Chứng minh được M A E ^ = A M E ^ (cùng = A B C ^ ) Þ AE = ME. Cmtt ta có AE = NE. Từ đó suy ra ME = NE.
c) Chứng minh EH//GF (//MB) và GE//FH (//NC) Þ EGFH là hình bình hành. Chứng minh được H E G ^ = B A C ^ = 90 0 ⇒ E G F H là hình chữ nhật. Suy ra GH đi qua trung điểm của EF.
S E G F H = H E . E G = 1 2 M B . 1 2 N C = 1 4 . 2 3 A B . 2 3 A C = 25 3 ( c m 2 )
Mà S E G F H = 4. S ⇒ I H F S I H F = 25 12 c m 2

a) Học sinh tự làm
b) Chứng minh A N 1 2 N C ⇒ S A M E = S A E N ⇒ E M = E N
hay E là trung điểm MN.
c) Chứng minh được EG//HF và HE/FG nên EHFG là hình bình hành; Mặt khác BM ^ NC (do AB ^ AC)
Suy ra EHFG là hình chữ nhật


Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

a) Ta có: MN // BC(gt) => \(\frac{AM}{AB}=\frac{AN}{AC}\)(theo định lí Ta - lét)
=> \(AN=\frac{AM}{AB}.AC=\frac{2,25}{6}\cdot8=3\)(cm)
=> \(CN=AC-AN=8-3=5\)
b) Ta có: MK // BI (gt) => \(\frac{MK}{BI}=\frac{AK}{AI}\)(theo định lí Ta - lét)
NK // IC (gt) => \(\frac{KN}{IC}=\frac{AK}{AI}\)(theo định lí Ta - lét)
=> \(\frac{MK}{BI}=\frac{KN}{IC}\) mà BI = IC (gt)
=> MK = KN => K là trung điểm của MN
c) Do BN là tia p/giác của góc ABC => \(\frac{AB}{BC}=\frac{AN}{NC}\)(t/c đường p/giác của t/giác)
=> \(BC=AB:\frac{AN}{NC}=6:\frac{3}{5}=10\)(cm)
Ta có: BC2 = 102 = 100
AB2 + AC2 = 62 + 82 = 100
=> BC2 = AB2 + AC2 => t/giác ABC vuông tại A (theo định lí Pi - ta - go đảo)
=> SABC = AB.AC/2 = 6.8/2 = 24 (cm2)

Hình bạn tự vẽ nhá
a) Ta có: MB = AB - AM = 6 - 2,25 = 3,75 (cm)
Gọi x là AN
NC là: 8 - x
Vì MN // BC, theo định lý Ta-lét ta có:
AMMB=ANNC⇔2,253,75=x8−x
⇔2,25(8−x)3,75(8−x)=3,75x3,75(8−x)
⇔2,25(8−x)=3,75x
⇔18−2,25x=3,75x
⇔−2,25x−3,75x=−18
⇔−6x=−18
⇔x=−18−6
⇔x=3
Nên NC = 8 - x = 8 - 3 = 5 (cm)
Vậy AN = 3cm, NC = 5cm
b) Ta có: MN // BC (gt) (1)
⇒ MK // BI, theo hệ quả của định lý Ta-lét ta có:
AKAI=MKBI (2)
Từ (1) ⇒ KN // IC, theo hệ quả của định lý Ta-lét ta có:
AKAI=KNIC (3)
Từ (2), (3) ⇒MKBI=KNIC(4)
Mà BI = IC (gt) (5)
Từ (4), (5) ⇒MK=KN
Nên K là trung điểm của MN

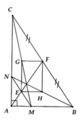
Câu 3: 3.5đ. Cho tam giác ABC có AB = 6cm, AC = 8 cm. TRên cạnh AB lấy điểm M sao cho AM = 2,25 cm. Qua M kẻ đường thẳng song song với BC cắt cạnh AC tại N
a) Tính độ dài các đoạn thẳng AN, CN.
b) Gọi I là trung điểm của BC, K là giao điểm của AI và MN. Chứng minh K là trung điểm của MN
. c) Nếu BN là tia phân gíac của góc ABC thì diện tích tam giác ABC là bao nhiêu?
a/quá dễ Pitago tìm AC rồi tìm S b/MN//BC nên \(\frac{ME}{BF}=\frac{AE}{AF}\left(1\right)\), và \(\frac{NE}{CF}=\frac{AE}{AF}\left(2\right)\)
(1)=(2) và BF=CF nên ME=NE
Cho O,D là tđ BM,NC(1)
(1) suy ra OD//BC( OD là đ/TB h/thang MNCB)(2)
Lại có I là tđ EF nên OI//BC ( OI là đ/TB h/thang MEFB)(3)
(2) và (3) suy ra O,I,D thẳng hàng (*)
Lại có G là tđ MC nên GD//MN( GD là đ/TB tgiac MNC) (4)
Lại có H là tđ BN nên OH//MN ( HO là đ/TB tgiac MNB) (5)
(4) ,(5) suy ra O,H,G,D nằm trên 1 đ/thẳng
Cộng với (*) suy ra ĐPCM