Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABC có \(BC^2=AB^2+AC^2\left(13^2=5^2+12^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
b) Xét ΔMKC và ΔMAB có
MK=MA(gt)
\(\widehat{CMK}=\widehat{BMA}\)(hai góc đối đỉnh)
MC=MB(M là trung điểm của BC)
Do đó: ΔMKC=ΔMAB(c-g-c)
c) Ta có: ΔMKC=ΔMAB(cmt)
nên \(\widehat{MKC}=\widehat{MAB}\)(hai góc tương ứng)
mà \(\widehat{MKC}\) và \(\widehat{MAB}\) là hai góc ở vị trí so le trong
nên AB//KC(Dấu hiệu nhận biết hai đường thẳng song song)
hay KC⊥AC
a, Ta có : \(\left\{{}\begin{matrix}AB^2+AC^2=169\\BC^2=169\end{matrix}\right.\)
\(\Rightarrow AB^2+AC^2=BC^2\)
=> Tam giác ABC vuông tại A .

a) Xét ΔMAB và ΔMKC có
MA=MK(gt)
\(\widehat{AMB}=\widehat{KMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔMAB=ΔMKC(c-g-c)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay BC=13(cm)
b) Xét ΔMKC và ΔMAB có
MK=MA(gt)
\(\widehat{KMC}=\widehat{AMB}\)(hai góc đối đỉnh)
MC=MB(M là trung điểm của BC)
Do đó: ΔMKC=ΔMAB(c-g-c)

Cho tam giác ABC có AB =5cm, AC=12cm, BC =13cm
a) Tam giác ABC có dạng đặc biệt gì? Tại sao?
b) Cho trung tuyến AM của tam giác ABC. Trên tia đối tia ÂM lấy K sao cho MK=MÀ. Chứng minh tam giác MKC=MBA từ đó suy ra KC vuông góc vs AC
c) Tinh AM

tự kẻ hình nghen:3333
a) ta có 13^2=169
5^2+12^2=25+144=169
=> 13^2=5^2+12^2
=> BC^2=AB^2+AC^2
=> tam giác ABC vuông tại A
b) Xét tam giác MKC và tam giác MBA có
AM=MK(gt)
BM=CM(gt)
KMC=BMA( đối đỉnh)
=> tam giác MKC= tam giác MBA( cgc)
=> CKM=MAB( hai góc tương ứng)
mà CKM so le trong với MAB=> KC//AB và AB vuông góc với AC=> KC vuông góc với AC
c) từ tam giác MKC=tam giác MBA=> AB=KC( hai cạnh tương ứng)
Xét tam giác BAC và tam giác KCA có
AB=KC(cmt)
AC chung
BAC=KCB(=90 độ)
=> tam giác BAC= tam giác KCA( cgc)
=> BC=AK( hai cạnh tương ứng)
=> 1/2 BC=1/2 AK
=> BM=CM=AM=KM
=> AM= BC/2=13/2=6,5cm

câu a: xét 2 tam giác MAB vs MCD :
ta có : AM = DM (gt)
góc BMA = góc DMC ( đối đỉnh)
MB = MC (gt)
=> tam giác MAB = tam giác MDC (c.g.c)
câu b: ta có : AC > AB
AB = CD ( 2 cạnh tương ứng)
=> AC > CD ( tính chất bắt cầu )
câu c: xét 2 tam giác ABK va ADK
ta có : AB = DC ( như câu a)
KA = KC ( gt )
=> tam giác ABK = tam giác CDK ( 2 cạnh góc vuông )
câu d : xét 2 tam giác NAK và ICK
ta có : AK = KC ( gt )
góc NAK = góc ICK (Vì :
*1: có góc A = góc C ( vuông )
*2:góc BAN = DCI ( như câu a)
từ *1 và *2 => góc A - góc BAN = góc NAK và góc C - góc DCI = góc ICK
=> góc NAK = góc ICK )
góc DKC = góc BKA ( như câu c )
=> tam giác NAK = tam giác ICK ( g.c.g )
=> NK = NI ( 2 cạnh tương ứng )
=> tam giác NKI cân tại K ( vì có NK = IK) .
Hy vọng nó đúng vì tui ko chắc ăn tam giác ACD có vuông hay ko . chúc bạn hc giỏi
d,CM AM<1/2(AB+AC).Điều này không đúng nếu tam giác ABC không là tam giác vuông.

a: Xét ΔMAB và ΔMKC có
MA=MK
góc AMB=góc KMC
MB=MC
=>ΔMAB=ΔMKC
b: ΔMAB=ΔMKC
=>góc MAB=góc MKC
=>AB//KC
=>KC vuông góc AC
=>góc ACK=90 độ
c: Xét ΔIAB vuông tại A và ΔICK vuông tại C có
IA=IC
AB=CK
=>ΔIAB=ΔICK
=>IB=IK
d: Xét ΔABC có CI/CA=CM/CB
nên IM//AB
=>IM vuông góc KB

a:
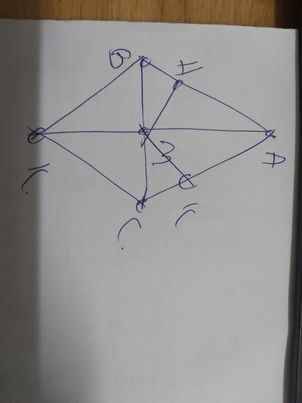
| GT | ΔABC cân tại A M là trung điểm của BC MK=MA MH\(\perp\)AB; MK\(\perp\)AC H\(\in\)AB; K\(\in\)AC |
| KL | b: ΔABM=ΔACM c: ΔABM=ΔKCM d: AB//CK e: MH=MK |
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
c: Xét ΔMAB và ΔMKC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMKC
d: Ta có: ΔMAB=ΔMKC
=>\(\widehat{MAB}=\widehat{MKC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//KC
e: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>MH=MK
=>ΔMHK cân tại M