Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

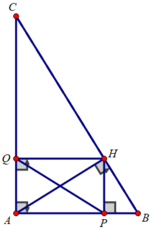
a) Xét tam giác ABC vuông tại A có:
A B 2 + A C 2 = B C 2
![]()
Tam giác ABC vuông tại A có AH là đường cao nên ta có:
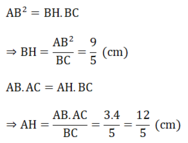
Ta có:
BH + CH = BC ⇒ CH = BC - BH = 5 - 9/5 = 16/5 (cm)

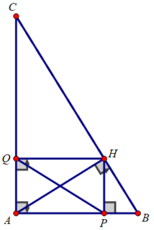
b)Xét tam giác ABC vuông tại A có:
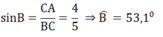
∠B + ∠C = 90 0 ⇒ ∠C = 90 0 - 53 , 1 0 = 36 , 9 0
Xét tứ giác APHQ có:
∠(PAQ) = ∠(AQH) = ∠(APH) = 90 0
⇒ Tứ giác APHQ là hình chữ nhật
⇒ PQ = AH = 12/5 (cm)

Bạn tự vẽ hình.
(a) \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
+) \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\hat{B}\approx53^o\)
+) \(\hat{C}=90^o-\hat{B}\approx90^o-53^o=37^o\)
(b) +) \(AB.AC=BC.AH\Leftrightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\)
\(\hat{A}=\hat{E}=\hat{F}=90^o\left(gt\right)\Rightarrow AEHF\) là hình chữ nhật.
Do đó, \(EF=AH\left(đpcm\right)\)

a: \(AB=\sqrt{3\cdot15}=3\sqrt{5}\left(cm\right)\)
\(AC=\sqrt{12\cdot15}=6\sqrt{5}\left(cm\right)\)
b: \(\dfrac{HF}{HE}=\dfrac{AE}{AF}=\dfrac{AH^2}{AB}:\dfrac{AH^2}{AC}=\dfrac{AC}{AB}=2\)
=>HF=2HE

\(a,AC=\sqrt{BC^2-AB^2}=3\sqrt{3}\left(cm\right)\\ \sin B=\dfrac{AC}{BC}=\dfrac{\sqrt{3}}{2}=\sin60^0\\ \Rightarrow\widehat{B}=60^0\\ \Rightarrow\widehat{C}=30^0\)
c) Xét tam giác AHB vuông tại H có HP là đường cao nên
AP.BP = HP 2
Xét tam giác AHC có HQ là đường cao nên
AQ.AC = HQ 2
Khi đó: AP.BP + AQ.AC = HP 2 + HQ 2 = PQ 2 (ΔPHQ vuông tại H)
⇒ AP.BP + AQ.AC = 12 / 5 2 = 5,76 cm