Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xet ΔBAC vuông tại A và ΔBHA vuông tại H có
góc B chung
=>ΔBAC đồng dạng vói ΔBHA
b: ΔABC vuông tại A có AH vuông góc BC
nên AB*AC=AH*BC
c: \(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
AH=6*8/10=4,8cm
CH=8^2/10=6,4cm

Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=8cm\)
Vì BE là pg \(\dfrac{AB}{BC}=\dfrac{AE}{EC}\Rightarrow\dfrac{EC}{BC}=\dfrac{AE}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{EC}{BC}=\dfrac{AE}{AB}=\dfrac{AC}{AB+BC}=\dfrac{8}{16}=\dfrac{1}{2}\Rightarrow EC=5cm;AE=3cm\)

a)
Xét tam giác BAC vuông tại A và tam giác BMN vuông tại M có:
\(\widehat{BAC}\)=\(\widehat{BMN}\)
=> Tam giác BAC ᔕ Tam giác BMN (g-g)
=> BA/BM=BC/BN
=> BN=BM.\(\dfrac{BC}{BA}\)=18.\(\dfrac{20}{12}\)=30cm
b)
Xét tam giác PAN vuông tại A và tam giác PMC vuông tại M có
\(\widehat{APN}\)=\(\widehat{MPC}\) (đối đỉnh)
=> Tam giác PAN ᔕ Tam giác PMC (g-g)
=> \(\dfrac{PA}{PM}\)=\(\dfrac{PN}{PC}\)
=> PA.PC=PM.PN (đpcm)

a: AC=8cm
b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: AH=4,8cm
bn ơi câu a bn giải thích ra luôn giùm mik ik
câu b,c nx

a: AC=căn 10^2-6^2=8cm
BM là phân giác
=>AM/AB=CM/BC
=>AM/3=CM/5=(AM+CM)/(3+5)=1
=>AM=3cm; CM=5cm
b: Xét ΔMAB vuông tại A và ΔMDC vuông tại D có
góc AMB=góc DMC
=>ΔMAB đồng dạng với ΔMDC
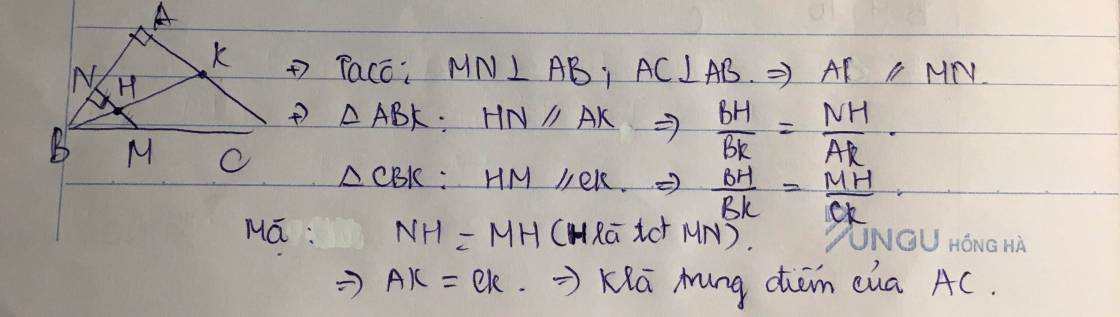
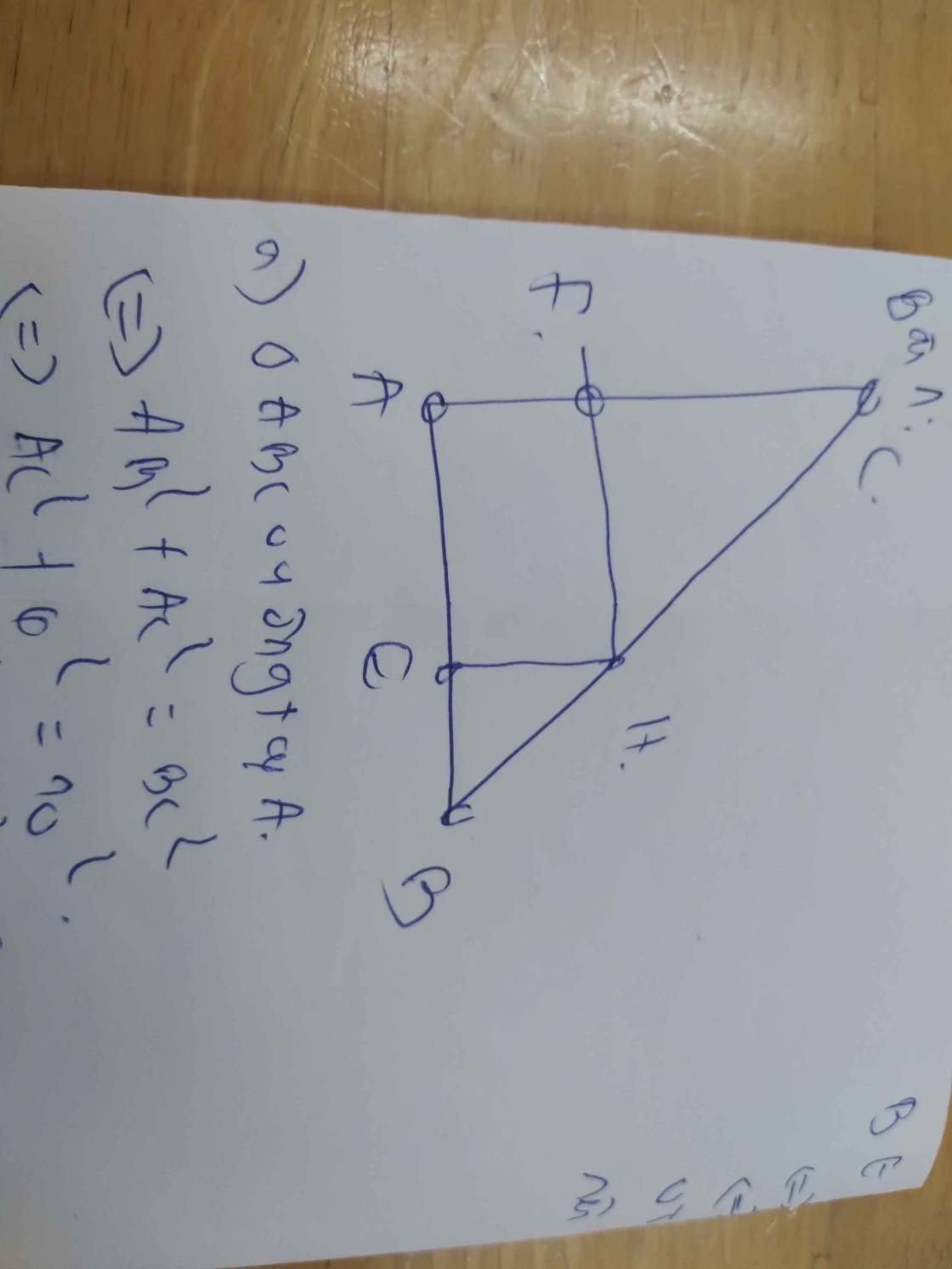



Áp dụng đinh lí Py-ta-go
AB2 + AC2 = BC2
62 + AC2 = 102
36 +AC2 = 100
AC2 = 100 - 36
AC2 = √ 64
AC = 8 (cm)
cj lớp 7 làm đc cả bài lớp 8 cơ à :v