Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác vuông ABC, áp dụng định lý Pi-ta-go ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\)
\(\Rightarrow BC=10\left(cm\right)\)
b) Xét tam giác BDC có AC là đường cao đồng thời trung tuyến nên BDC là tam giác cân tại C.
c) Xét tam giác cân BDC có CA là đường cao nên đồng thời là phân giác.
Vậy thì \(\widehat{HCA}=\widehat{KCA}\)
Xét tam giác vuông AHC và tam giác vuông AKC có:
Cạnh huyền AC chung
\(\widehat{HCA}=\widehat{KCA}\)
\(\Rightarrow\Delta AHC=\Delta AKC\) (Cạnh huyền - góc nhọn)
d) Do \(\Delta AHC=\Delta AKC\Rightarrow HC=KC\)
Suy ra tam giác HKC cân tại C. Vậy thì phân giác CA đồng thời là đường cao, hay \(CA\perp HK\)
Lại có \(CA\perp BD\) nên HK // BC.

a: BC=15cm
b: Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
DO đó: ΔCBD cân tại C
c: Xét ΔCHA vuông tại H và ΔCKA vuông tại K có
CA chung
\(\widehat{HCA}=\widehat{KCA}\)
Do đó: ΔCHA=ΔCKA
d: Xét ΔCDB có CK/CD=CH/CB
nên HK//DB

b) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)

a: \(BC=\sqrt{34}\left(cm\right)\)
b: Xét ΔBCD có
CA là đường cao
CA là đường trung tuyến
Do đó:ΔCBD cân tại C
c: Xét ΔCKA vuông tại K và ΔCHA vuông tại H có
CA chung
\(\widehat{KCA}=\widehat{HCA}\)
Do đó: ΔCKA=ΔCHA
Suy ra: CK=CH
d: Xét ΔCBD có CK/CD=CH/CB
nên HK//BD

Áp dụng định lí Py-ta-go vào △ABC, Ta có
\(AB^2+AC^2=BC^2\)
\(\Rightarrow9^2+12^2=BC^2\Leftrightarrow81+144=BC^2=225\)
\(\Rightarrow BC=15\)

a: Sửa đề: AC=12cm
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=5^2+12^2=169\)
=>\(BC=\sqrt{169}=13\left(cm\right)\)
b:
Ta có: AB và AE là hai tia đối nhau
=>A nằm giữa B và E
mà AB=AE
nên A là trung điểm của BE
Xét ΔCBE có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCBE cân tại C
c: Ta có: ΔCBE cân tại C
mà CA là đường cao
nên CA là phân giác của góc ECB
Xét ΔCIA vuông tại I và ΔCHA vuông tại H có
CA chung
\(\widehat{ICA}=\widehat{HCA}\)
Do đó: ΔCIA=ΔCHA
d: Ta có: ΔCIA=ΔCHA
=>CI=CH
Xét ΔCEB có \(\dfrac{CI}{CE}=\dfrac{CH}{CB}\)
nên HI//EB

a: BC=15cm
b: Xét ΔCDB có
CA là đường cao
CA là đường trung tuyến
Do đó:ΔCDB cân tại C

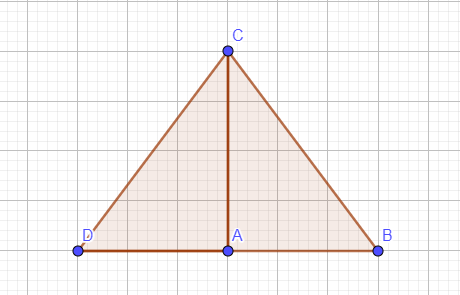
`a)` Áp dụng định lý pytago ta có :
`AB^2+AC^2=BC^2`
hay `9^2+12^2=BC^2`
`=>BC^2=225`
`=>BC=15(cm)`
`b)` Xét `ΔABC` và `ΔADC` ta có :
`AC` chung
`\hat{BAC}=90^o`
`\hat{DAC}=90^o`
`=>ΔABC=ΔADC` (c.g.c)
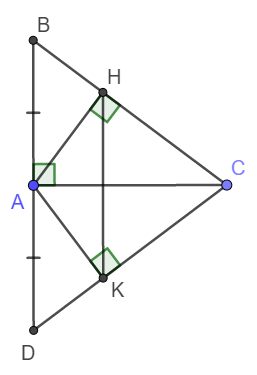

ta có \(BC=\sqrt{AB^2+AC^2}=15cm\)
Xét tam giác BCD có CA vừa là đường cao vừa là đường trung tuyến nên BCD cân tại C
Nên CA cũng là tia phân giác \(\Rightarrow\hept{\begin{cases}\widehat{ACH}=\widehat{ACK}\\\widehat{AHC}=\widehat{AKC}=90^0\\AC\text{ chung}\end{cases}}\) vậy AHC=AKC theo trường hợp cạnh huyền góc nhọn