Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc BAH+góc B=90 độ
góc ACB+góc B=90 độ
=>góc BAH=góc ACB
Xét ΔADB có
AH vừa là đường cao, vừa là trung tuyến
=>ΔADB cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAD
=>góc HAD=góc ACB
=>góc ACB=góc ECB
=>CB là phân giác của góc ACE

câu d:
Tam giác BCF nội tiếp (O;BC/2) có cạnh BC là đường kính
=> Tam giác BCF vuông tại F
=>góc BFC=90 độ
Xét 2 tam giác: tam giác CHF và tam giác CFB có:
góc C chung
góc CHF=góc CFB (=90 độ)
Do đó, tam giác CHF đồng dạng với tam giác CFB (g.g)
=> góc CFH=góc CBF (1)
Tứ giác ABFC nội tiếp (O;BC/2)
=> góc CFH=góc ABC (cùng chắn cung AC) (2)
Từ (1) và (2)=> góc CBF=góc ABC (3)
Mà tia BC nằm giữa tia AB và BF (4)
Từ (3) và (4)=> BC là tia phận giác của góc ABF (đpcm)

GIẢI: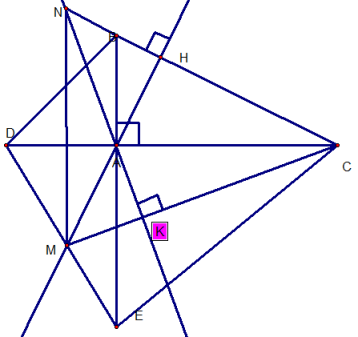
a) Xét Δ ABC và Δ AED, ta có :
(đối đỉnh)
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
(Δ ABC vuông tại A)
=> AD AE
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : ở vị trí so le trong
=> BD // CE
b) Xét Δ MNC, ta có :
NK MC = > NK là đường cao thứ 1.
MH NC = > MH là đường cao thứ 2.
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN AC tại I.
mà : AB AC
=> MN // AB.
c) Xét Δ AMC, ta có :
(đối đỉnh)
(Δ ABC = Δ AED)
=> (cùng phụ góc ABC)
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
(MN
AC tại I)
IM cạnh chung.
mặt khác : (so le trong)
(đồng vị)
mà : (cmt)
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.
c)
\(\widehat{ECH}=\widehat{HCA}\left(câub\right)\)
Tg AHCE nt \(\Rightarrow\widehat{HEA}=\widehat{HCA}\)
\(\Rightarrow\widehat{ECH}=\widehat{HEA}\)
xét ΔHDE và ΔHEC
\(\widehat{H}\) chung
\(\widehat{HED}=\)\(\widehat{ECH}\)
⇒ΔHDE ∼ΔHEC (g.g)
\(\dfrac{HE}{HC}=\dfrac{HD}{HE}\Leftrightarrow HE^2=HC\cdot HD\left(đpcm\right)\)