Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
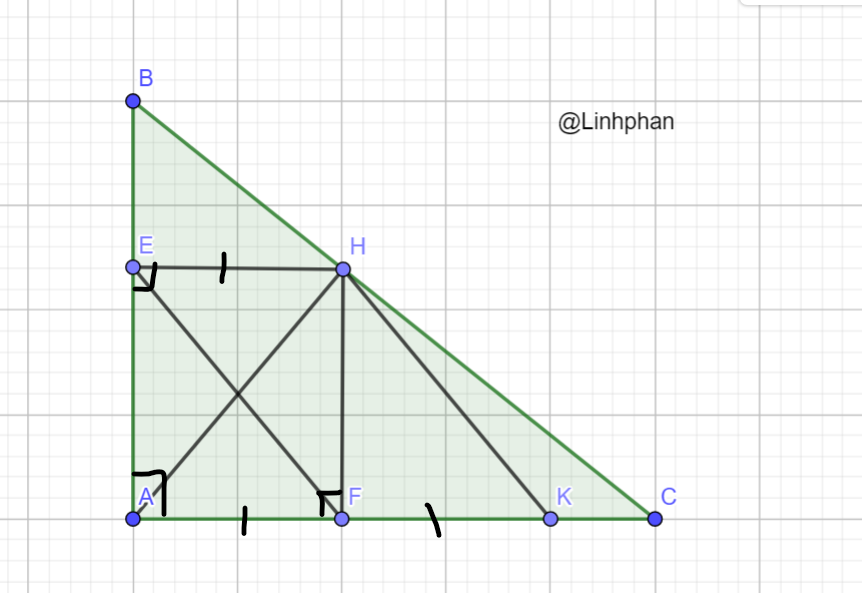
a, Xét tứ giác AEHF có : ^AEH = ^EAF = ^HFA = 900
Vậy tứ giác AEHF là hcn
=> AH = EF ( 2 đường chéo bằng nhau )
c, Theo Pytago tam giác ABC vuông tại A
\(AB=\sqrt{BC^2-AC^2}=3cm\)
SABC = 1/2 . AB . AC = 1/2 . 3 . 4 = 6 cm2
a) Xét tứ giác AEHF:
\(\widehat{EAF}=90^o;\widehat{AEH}=90^o;\widehat{AFH}=90^o\)
(Do tam giác ABC vuông tại A; HE và HF lần lượt vuông góc với AB và AC).
=> AEHF là hình chữ nhật (dhnb).
=> AH = EF (Tính chất 2 đường chéo của hình chữ nhật).
b) Ta có: FK = AF (gt).
Mà AF = EH (AEHF là hình chữ nhật).
=> AF = EH = FK.
Ta có: EH // AF (AEHF là hình chữ nhật).
Mà F thuộc AK (gt).
=> EH // FK.
Xét tứ giác EHKF:
EH // FK (cmt).
EH = FK (cmt).
=> EHKF là hình bình hành (dhnb).
c) Xét tam giác ABC vuông tại A:
Ta có: BC2 = AB2 + AC2 (Định lý Pytago).
Thay số: 52 = AB2 + 42.
=> AB2 = 9. => AB = 3.
Diện tích tam giác ABC vuông tại A:
\(\dfrac{1}{2}AB.AC=\dfrac{1}{2}.3.4=6\left(cm^2\right).\)
a, Vì HE ⊥ AB ; FA ⊥ AB => HE // FA (từ ⊥ đến // )
+, EA ⊥ AC ; HF ⊥ AC => EA // HF (từ ⊥ đến // )
Xét tứ giác AEHF có: HE // FA (cmt) ; EA // HF (cmt)
=> Tứ giác AEHF là hình bình hành (dhnb)
mà \(\hat{EAF} =90^0\)
=> Tứ giác AEHF là hình chữ nhật
=> AH = EF
b, Vì AEHF là hình chữ nhật (cmt)
=> EH//AF; EH = AF mà AF= FK (gt)
=> EH = FK
+, Xét tứ giác EHKF có: EH = FK (cmt)
EH // FK (do EH // AF; K ∈ AF)
=> Tứ giác EHKF là hình bình hành (dhnb)
Mình chỉ giải c thôi nhé :) Phần a, b nếu ai muốn biết hỏi @Nấm Chanel
A B C H E F K O I
Có \(\widehat{HEA}=\widehat{BAC}=90^o\) nên \(EH\text{//}AC\) hay \(EH\text{//}FK\)
Đồng thời tứ giác \(EHFA\) có 3 góc vuông nên là hình chữ nhật, tức EH = FA ( 2 cạnh đối ), mà AF = FK ( giả thiết ) nên EH = FK
Từ đó suy ra tứ giác EHKF là hình bình hành nên EK cắt HF tại trung điểm mỗi đường, hay I là trung điểm EK (1)
Đồng thời hình chữ nhật EHFA có hai đường chéo EF và AH cắt nhau tại O, nên O là trung điểm EF ( tính chất hình chữ nhật ) (2)
(1)(2)\(\Rightarrow\)OI là đường trung bình \(\Delta EKF\) , suy ra OI // FK, hay OI // AC
Vậy ...
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
b: Xét tứ giác EHKF có
EH//KF
EH=KF
Do đó: EHKF là hình bình hành
c: Ta có: AEHF là hình chữ nhật
mà O là giao điểm của hai đường chéo
nên O là trung điểm chung của AH và EF
Ta có: HEFK là hình bình hành
nên Hai đường chéo HF và KE cắt nhau tại trung điểm của mỗi đường
=>I là trung điểm chung của HF và KE
Xét ΔKEF có
I là trung điểm của KE
O là trung điểm của FE
Do đó: IO là đường trung bình
=>IO//KF
hay IO//AC
a) Tứ giác AEHF là hình chữ nhật vì có 3 góc vuông
Nên AH = EF (hai đường chéo của hình chữ nhật)
b) AEHF là hình chữ nhật nên EH = AF ; EH song song với AK
Mà FK = AF nên EH = FK
Tứ giác EHKF có EH song song và bằng FK nên là hình bình hành
1: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
2: Xét tứ giác EHKF có
EH//KF
EH=KF
Do đó: EHKF là hình bình hành
3: Vì AEHF là hình chữ nhật
nên AH cắt FE tại trung điểm của mỗi đường
=>O lf trung điểm chung của AH và FE
Vì EHKF là hình bình hành
nên EK cắt HF tại trung điểm của mỗi đường
=>I lf trung điểm của EK và HF
Xét ΔEKF có EO/EF=EI/EK
nên OI//KF
=>OI//AC
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=EF
b: Ta có: AEHF là hình chữ nhật
=>HE//AF và HE=AF
Ta có: HE//AF
F\(\in\)AK
Do đó: HE//KF
Ta có: HE=AF
AF=FK
Do đó: HE=KF
Xét tứ giác HEFK có
HE//FK
HE=FK
Do đó: HEFK là hình bình hành
c: Ta có: AEHF là hình chữ nhật
=>AH cắt EF tại trung điểm của mỗi đường
=>O là trung điểm chung của AH và EF
Ta có: HEFK là hình bình hành
=>HF cắt EK tại trung điểm của mỗi đường
=>I là trung điểm chung của HF và ÊK
Xét ΔEKF có
O,I lần lượt là trung điểm của EF,EK
=>OI là đường trung bình của ΔEKF
=>OI//KF
=>OI//AC