Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M 5cm 12cm
a, Áp dụng định lí Piatago trong \(\Delta ABC\) vuông tại \(A\) có:
\(\Rightarrow BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=5^2+12^2\)
\(\Rightarrow BC=\sqrt{169}\)
\(\Rightarrow BC=13cm\)
Ta có: \(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\) nên:
\(\Rightarrow AM=\frac{1}{2}BC=\frac{1}{2}.13=6,5cm\)
b, Xét tứ giác \(ABCD\) có:
\(M\) là trung điểm của \(AD\)
\(M\) là trung điểm của \(BC\)
\(\Rightarrow ABCD\) là HBH
\(\Rightarrow AD=BC\)
c, Giả sử \(AB=AC\)
\(\Rightarrow\Delta ABC\)vuông cân ( Từ đầu \(\Delta ABC\) vuông rồi)
Xét HBH \(ABCD\) có:
\(\widehat{A}=90^0\)
\(\Rightarrow ABCD\) là HCN
Xét hình chữ nhật \(ABCD\) có:
\(AB=AC\left(gt\right)\)
\(\Rightarrow ABCD\) là hình vuông.
Để \(ABCD\) là hình vuông thì \(\Delta ABC\) vuông tại \(A\) cần thêm điều kiện \(AB=AC\)
M A B C D
a ) Xét \(\Delta ABC\)vuông tại A (gt) có :
\(BC^2=AB^2+AC^2\)( định lý Py - ta - go )
\(BC^2=5^2+12^2\)
\(BC^2=25+144\)
\(BC^2=169\)
\(\Rightarrow BC=13cm\)( vì BC > 0 )
+ Vì AM là đường trung tuyến ứng với cạnh huyền BC trong tam giác vuông ABC ( gt)
\(\Rightarrow AM=\frac{1}{2}BC\)( tính chất tam giác vuông cân )
\(\Rightarrow AM=\frac{1}{2}.13\)
\(\Rightarrow AM=6,5\left(cm\right)\)
b ) Vì AM là đường trung tuyến của \(\Delta ABC\left(gt\right)\)
\(\Rightarrow M\)là trung điểm của BC (1)
+ Vì D đối xứng với A qua M (gt)
\(\Rightarrow M\)là trung điểm của AD (2)
Từ (1) và (2) \(\Rightarrow\) 2 dường chéo BC và AD cắt nahu tại trung điểm M của mỗi đường
\(\Rightarrow\)Tứ giác \(ABCD\) là hình bình hành ( dấu hiệu nhận biết hình bình hành )
Mà \(\widehat{BAC}=90^0\left(gt\right)\)
\(\Rightarrow\)Hình bình hành ABCD là hình chữ nhật ( dấu hiệu nhận biết hình chữ nhật )
\(\Rightarrow AD=BC\)( tính chất hình chữ nhật )
c ) Theo câu b ta có \(ABCD\)là hình chữ nhật
Để hình chữ nhật \(ABCD\) là hình vuông
\(\Leftrightarrow AB=AC\)
\(\Rightarrow\Delta ABC\)cân tại A
Mà \(\Delta ABC\)vuông tại A (gt)
\(\Rightarrow\Delta ABC\)vuông cân tại A .
Vậy \(\Delta ABC\)vuông cân tại A thì hình chữ hật ABCD là hình vuông
Chức bạn học tốt !!!

a ) BC = 13 cm
AM = 6,5 cm
b) ta có
tam giác ABC vuông tại A , AM là trung tuyến
nên BC = 2AM
mà D đối xứng với A qua M
nên AD = 2 AM
suy ra : BC =AM
c) để ABCD là hình vuông thì tam giác ABC phải vuông cân

a) Xét tứ giác ABCD có:
. M là trung điểm của BC ( AM là đường trung tuyến)
. M là tđ của AD ( gt)
Vậy: ABCD là hbh ( tứ giác có 2 đường chéo cắt nhau tại tđ của mỗi đường)
mà \(\widehat{BAC}\) = 900 ( \(\Delta\) ABC vuông tại A)
--> ABCD là hình chữ nhật ( hbh có 1 góc vuông)
b) Ta có: \(IA\perp AC\)
\(CD\perp AC\)
\(\Rightarrow\) IA // CD
Xét tứ giác BIDC có:
. IA // CD (cmt)
\(\Rightarrow\) IB // CD ( B ϵ IA )
. AB =CD ( cạnh đối hcn ABCD )
mà AB = IB ( tính chất đối xứng)
\(\Rightarrow\) IB = CD ( cùng = AB )
Vậy: BIDC là hbh ( tứ giác có 2 cạnh đối vừa //, vừa = nhau)
\(\Rightarrow\) BC // ID ( cạnh đối hbh)
" đề câu c sai nha bạn"

Bạn tự vẽ hình nha !
a) Theo đề, ta có:
N là điểm đối xứng với M qua I
mà I là trung điểm của AC hay I thuộc AC
=> N đối xứng với M qua AC.
b) Xét tam giác ABC có:
BM = CM (gt)
AI = CI (gt)
=> MI là đường trung bình của tam giác ABC
=> MI//AB
mà AB vuông góc với AC
=> MI vuông góc AC
Xét tứ giác ANCM có:
MI = NI (gt)
AI = CI (gt)
=> tứ giác ANCM là hình bình hành có MI vuông góc với AC
=> ANCM là hình thoi
c) Hình thoi ANCM là hình vuông khi đường chéo AM là phân giác của góc A
Tam giác ABC có AM vừa là phân giác vừa là trung tuyến nên tam giác ABC cân tại A .
Vậy điều kiện để ANCM là hình vuông là tam giác ABC vuông cân tại A.
XONG!!! ![]()
![]()

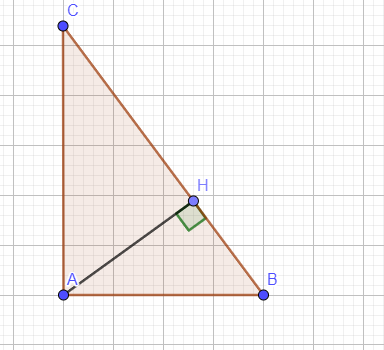
Áp dụng định lý pytago ta có :
`AC^2+AB^2=BC^2`
hay `16^2+12^2=BC^2`
`=>BC^2=400`
`=>BC=20(cm)`

Bạn tự vẽ hình nhé!
a) Xét tam giác ADC và tam giác BEC có:
\(\widehat{C}\)chung
\(\frac{CD}{CE}=\frac{CA}{CB}\)(2 tam giác vuông CDE và CAB đồng dạng)
=> Tam giác ADC đồng dạng với tam giác BEC (cgc) (đpcm)
b) Tam giác AHD vuông tại H (gt)
=> \(\widehat{BEC}=\widehat{ADC}=135^o\)
Nên \(\widehat{AEB}=45^o\)do đó tam giác ABE vuông tại A
=> BE=\(AB\sqrt{2}=3\sqrt{2}\)
Nguồn: Đặng Thị Nhiên
c) Tam giác ABE vuông tại A nên tia AM là phân giác BAC
\(\Rightarrow\frac{GB}{GC}=\frac{AB}{AC}\)
Vì tam giác ABC đồng dạng tam giác DEC nên:
\(\frac{AB}{AC}=\frac{ED}{DC}=\frac{AH}{HC}=\frac{HD}{HC}\)(DE//AH)
Do đó: \(\frac{GB}{GC}=\frac{HD}{HC}\Rightarrow\frac{GB}{GB+GC}=\frac{HD}{HD+HC}\Rightarrow\frac{GB}{GC}=\frac{AH}{AH+HC}\left(đpcm\right)\)
Nguồn: Đặng Thị Nhiên

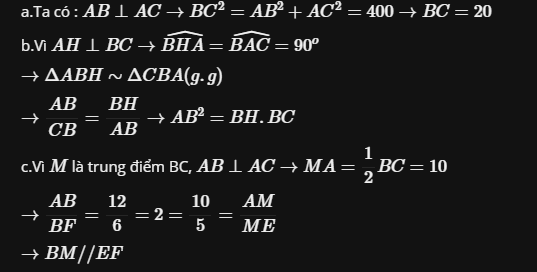
A B C M 5 12
a) \(BC^2=AC^2+AB^2=5^2+12^2=169=13^2\)
=> \(BC=13\)
Theo tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông thì
\(AM=\frac{1}{2}BC=\frac{13}{2}=6,5\)
b) ABDC là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường. Hơn nữa góc A vuông nên ABDC là hình chữ nhật. Suy ra hai đường chéo bằng nhau, AD = BC
c) Để ABDC là hình vuông thì AB = AC => Tam giác ABC là vuông cân.
a) BC^2=AC^2+AB^2=5^2+12^2=169=13^2
=> BC=13
Theo tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông thì
AM=12 BC=132 =6,5
b) ABDC là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường. Hơn nữa góc A vuông nên ABDC là hình chữ nhật. Suy ra hai đường chéo bằng nhau, AD = BC
c) Để ABDC là hình vuông thì AB = AC => Tam giác ABC là vuông cân.