Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

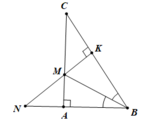
Tự vẽ hình nhé ?
a) Xét ∆ABM và ∆KBM có :
Góc BAM = BKM (do AB ⊥ AC, MK ⊥ BC (GT))
BM chung
Góc ABM = KBM (do BM là tia pg của góc ABC (GT))
=> ∆ABM = ∆KBM (ch - gn) (1)
=> Góc AMB = KMB (2 góc tương ứng)
Mà MB nằm giữa MA và MK
=> MB là tia pg của góc AMK (đpcm)
b) Từ (1) => AM = KM (2 cạnh tương ứng) (2)
Ta có : Góc BAM (=90o) + NAM = 180o (kề bù)
Mà góc BKM (=90o) + CKM = 180o (kề bù)
=> Góc NAM = CKM (3)
Xét ∆ANM và ∆KCM có :
Góc AMN = CMK (đối đỉnh)
AM = KM (Theo (2))
Góc NAM = CKM (Theo (3))
=> ∆ANM = ∆KCM (g.c.g)
=> MN = MC (2 cạnh tương ứng)
Vậy...

c. Do tam giác MKC vuông tại K nên MK < MC (0.5 điểm)
Mà MA = MK ⇒ MA < MC (0.5 điểm)

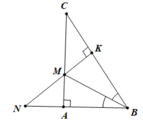
d. Trong tam giác ANC có hai đường cao CA và NK cắt nhau tại M nên M là trực tâm tam giác ANC (0.5 điểm)
Suy ra BM cũng là đường cao của tam giác ANC
BM vuông góc với CN (0.5 điểm)

a. Hình vẽ (0.5 điểm)
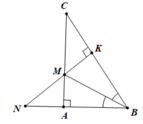
Xét ΔABM và ΔKBM có:
∠(ABM) = ∠(KBM)
BM là cạnh chung
⇒ ΔABM = ΔKBM(cạnh huyên – góc nhọn) (1 điểm)
⇒ AM = MK và BA = BK (hai cạnh tương ứng) ⇒ M, B nằm trên đường trung trực của AK (0.5 điểm)
Suy ra BM là đường trung trực của AK

Làm
a) Xét hai tam giác vuông ABM và tam giác vuông KBM có :
BM là cạnh chung
góc ABM = góc KBM ( gt )
Do đó : Tam giác ABM = tam giác KBM ( cạnh huyền - góc nhọn )
=> BA = BK nên B thuộc đường trung trực của AK
MA = MK nên K thuộc đường trung trực của AK
Vậy BM là đường trung trực của AK
b) Xét hai tam giác vuông AMN và tam giác KMC có :
góc AMN = góc KMC ( đối đỉnh )
MA = MK ( theo câu a )
Do đó : tam giác AMN = KMC ( cạnh góc vuông - góc nhọn )
Vậy MC = MN
c) Phần c không dõ đề bài nên mk k giải đc câu c nếu muốn giải câu c thì cậu gửi đề bài cho mk mk giải cho
d) Ta có : AB + AN = BN
BK + KC = BC
Mà BA = BK ( theo câu a )
AN = KC ( Theo câu b )
=> BN = BC ( *)
Xét tam giác NBM và tam giác CBM có :
BM là cạnh chung
BN = BC ( theo *)
góc NBM = góc CBM ( gt )
Do đó : tam giác NBM = tam giác CBM ( c.g.c )
=> góc BMN = góc BMC
mà góc BMN + góc BMC = 180°
=> góc BMN = góc BMC = 180° : 2
=> góc BMN = góc BMC = 90°
Vậy BM vuông hóc với NC
HỌC TỐT
Hình bn tự vẽ nhé
a. Xét hai tam giác vuông ABM và tam giác vuông KBM có;
góc BAM = góc BKM = 90độ
cạnh BM chung
góc ABM = góc KBM [ vì BM là tia pg góc B ]
Do đó ; tam giác ABM = tam giác KBM [ cạnh huyền - góc nhọn ]
\(\Rightarrow\)AB = KB nên B \(\in\)đường trung trực của AK
và MA = MK nên M \(\in\)đường trung trực của AK
\(\Rightarrow\)BM là đường trung trực của AK
b.Xét hai tam giác vuông AMN và tam giác vuông KMC có ;
góc MAN = góc MKC = 90độ
AM = KM [ theo câu a ]
góc AMN = góc KMC [ đối đinh ]
Do đó ; tam giác AMN = tam giác KMC [ cạnh góc vuông - góc nhọn ]
\(\Rightarrow\)MN = MC [ cạnh tương ứng ]
c.Theo câu a ; tam giác ABM = tam giác KBM
\(\Rightarrow\)AM = KM [ cạnh tương ứng ] [ 1 ]
Xét tam giác KMC vuông tại K nên ;
MK bé hơn MC [ 2 ]
Từ [ 1 ] và [ 2 ] suy ra ;
AM bé hơn MC
d. Theo câu b ; tam giác AMN = tam giác KMC
\(\Rightarrow\)AN = KC [ cạnh tương ứng ]
mà BA = BK [ vì tam giác ABM = tam giác KBM theo câu a ]
\(\Leftrightarrow\)AN + BA = KC + BK
\(\Rightarrow\) BN = BC nên B thuộc đường trung trực của CN
mà MN = MC nên M thuộc đường trung trực của CN
Vậy BM thuộc đường trung trực của CN
\(\Rightarrow\)BM vuông góc với CN
Theo mk nghĩ thì câu c . So sánh AM với MC
d. BM vuông góc với CN
HỌC TỐT
Nhớ kb với mk nha

a: Xét ΔCAM vuông tại A và ΔCNM vuông tại N có
CM chung
góc ACM=góc NCM
=>ΔCAM=ΔCNM
b: Xét ΔMAK vuông tại A và ΔMNB vuông tại N có
MA=MN
góc AMK=góc NMB
=>ΔMAK=ΔMNB
=>MK=MB

a: Xẻt ΔCAM vuông tại A và ΔCNM vuông tại N có
CM chung
góc ACM=góc NCM
=>ΔCAM=ΔCNM
b: Xét ΔMAK vuông tại A và ΔMNB vuông tại N có
MA=MN
góc AMK=góc NMB
=>ΔMAK=ΔMNB
=>MK=MB

4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.

hinh tu ve :
Xet tamgiac AFN va tamgiac AEN co :
FE | AM (gt) => goc FNA = goc ANE = 90 do (dn) (1)
AN la tia phan giac cua goc CAB (gt) => goc FAN = goc NAE (dn) (2)
AN chung (3)
(1)(2)(3) => tamgiac AFN = tamgiac AEN (cgv - gnk)
=> AE = AF (dn)
b, ke BO = BE (O thuoc FE)
b. Xét ΔAMF và ΔKMC có:
AM = MK
∠(AMN) = ∠(KMC) (hai góc đối đỉnh)
⇒ ΔAMF = ΔKMC ( cạnh góc vuông – góc nhọn kề) (0.5 điểm)
⇒ MN = MC (hai cạnh tương ứng) (0.5 điểm)