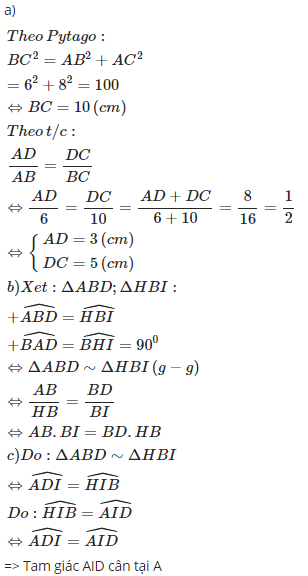Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

e) \(AH\perp BC\)(giả thiết).
\(\Rightarrow\Delta HAB\)vuông tại H.
\(\Rightarrow S_{HAB}=\frac{AH.BH}{2}=4,8.\frac{30}{14}=\frac{144}{14}=\frac{72}{7}\left(cm^2\right)\)
Xét \(\Delta ABC\)có phân giác BD (giả thiết).
\(\Rightarrow\frac{AD}{CD}=\frac{AB}{BC}\)(tính chất).
\(\Rightarrow\frac{AD}{CD+AD}=\frac{AB}{BC+AB}\)(tính chất của tỉ lệ thức).
\(\Rightarrow\frac{AD}{AC}=\frac{AB}{BC+AB}\)
\(\Rightarrow\frac{AD}{8}=\frac{6}{10+6}=\frac{6}{16}=\frac{3}{8}\)(thay số).
\(\Rightarrow AD=\frac{3}{8}.8=3\left(cm\right)\)
Vì \(\Delta ABC\)vuông tại A (giả thiết).
\(\Rightarrow\widehat{CAB}=90^0\Rightarrow\widehat{DAB}=90^0\)
\(\Rightarrow\Delta ADB\)vuông tại A.
\(\Rightarrow S_{ADB}=\frac{AD.AB}{2}=\frac{3.6}{2}=9\left(cm^2\right)\)
Ta có: \(S_{ABC}=\frac{AB.AC}{2}\)(theo câu a))
\(\Rightarrow S_{ABC}=\frac{6.8}{2}=\frac{48}{2}=24\left(cm^2\right)\)
Lại có: \(S_{ABD}+S_{BCD}=S_{ABC}\)
\(\Rightarrow9+S_{BCD}=24\)(thay số).
\(\Rightarrow S_{BCD}=24-9=15\left(cm^2\right)\)
Vậy \(S_{HAB}=\frac{72}{7}cm^2;S_{BCD}=15cm^2\)

:a) Xét tam giác ABC có BC2=AB2+AC2 ( Định lý Py-ta-go)
Thay số:BC2=6 2+8 2 BC2=36+64=100 =>BC=10(cm)
b) Vì BI là phân giác => góc ABI= góc HBI= góc ABC / 2
Xét tam giác ABI vuông tại A và tam giác HBI vuông tại H có:
Bi chung, góc ABI= góc HBI ( cmt) => tam giác ABI= tam giác HBI (cạnh huyền - góc nhọn)

Mk chỉnh lại đề câu b: Chứng minh: \(AB^2=BH.BC\) hoặc \(HA^2=HB.HC\)
a) Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow\)\(BC^2=6^2+8^2=100\)
\(\Rightarrow\)\(BC=\sqrt{100}=10\)
b) Xét \(\Delta ABH\)và \(\Delta CBA\)có:
\(\widehat{B}\) chung
\(\widehat{AHB}=\widehat{CAB}=90^0\)
suy ra: \(\Delta ABH~\Delta CBA\)(g.g)
\(\Rightarrow\)\(\frac{AB}{BC}=\frac{BH}{AB}\) \(\Rightarrow\)\(AB^2=BH.BC\)
Chứng minh: \(AH^2=HB.HC\) thì c/m: \(\Delta HAB~\Delta HCA\)(g.g)
\(\Rightarrow\)\(AB^2=BH.BC\)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy:BC=10cm

a)Xét tam giác ABC vuông tại A(gt),có:
AB^2+AC^2=BC^2(Đl pytago)
Thay số:36+64=BC^2
=>BC= căn 100=10cm
Xét tam giác ABC có BD là phân giác góc ABC(gt),có:
AB/AC=AD/DC(Tính chất đường phân giác trong tam giác)
<=>AB/AB+AC=AD/AD+DC(Tính chất tỉ lệ thức)
Thay số:6/16=AD/8
<=>16AD=48
<=>AD=3cm
Vì D thuộc AC(gt)
=>AD+DC=AC
Thay số:3+DC=8
<=>DC=5cm
b) Xét tam giác ABC vuông tại A(gt),có:
SABC=(AB.AC)/2=24cm^2
Mà SABC=(AH.BC)/2
=>(AH.10)/2=24
<=>AH=24.2÷10=4,8cm
Xét tam giác ABC đồng dạng tam giác HAC có:
+Góc C chung
+Góc AHC=góc BAC=90 độ
=>tam giác ABC đồng dạng tam giác HAC(g.g)
=> AH/AB=CH/AC(Cặp cạnh tương ứng)
Thay số : 4,8/6=CH/8
=>CH=4,8.8÷6=6,4cm
c)

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
BD là phân giác
=>DA/AB=DC/AC
=>DA/3=DC/5=(DA+DC)/(3+5)=8/8=1
=>DA=3cm; DC=5cm
b: IH/IA=BH/BA
AD/DC=BA/BC
mà BH/BA=BA/BC
nên IH/IA=AD/DC

a) Xét \(\Delta BAH\) và \(\Delta BCA\)có:
\(\widehat{B}\) chung
\(\widehat{BHA}=\widehat{BAC}=90^0\)
suy ra: \(\Delta BAH~\Delta BCA\) (g.g)
\(\Rightarrow\)\(\frac{AB}{BC}=\frac{BH}{AB}\)
\(\Rightarrow\)\(AB^2=BH.BC\)
c) Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow\)\(BC=10\)
\(\Delta ABC\)có AK là phân giác
\(\Rightarrow\)\(\frac{KB}{AB}=\frac{KC}{AC}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{KB}{AB}=\frac{KC}{AC}=\frac{KB+KC}{AB+AC}=\frac{5}{7}\)
suy ra: \(KB=\frac{30}{7}\) \(KC=\frac{40}{7}\)
c) Xét \(\Delta ABD\)và \(\Delta HBI\)có:
\(\widehat{ABD}=\widehat{HBI}\) (gt)
\(\widehat{BAD}=\widehat{BHI}=90^0\)
suy ra: \(\Delta ABD~\Delta HBI\)
\(\Rightarrow\)\(\frac{AB}{HB}=\frac{BD}{BI}\)
\(\Rightarrow\)\(AB.BI=BD.HB\)
d) \(S_{ABC}=\frac{1}{2}.AB.AC=24\)
\(\Delta ABH~\Delta CBA\) (câu a)
\(\Rightarrow\)\(\frac{S_{ABH}}{S_{CBA}}=\left(\frac{AB}{BC}\right)^2=\frac{9}{16}\)
\(\Rightarrow\)\(S_{ABH}=\frac{9}{16}.S_{ABC}=13,5\)
â) chứng minh AB2 = BH . BC
Xét : \(\Delta ABHva\Delta ABC,co\):
\(\widehat{B}\) là góc chung
\(\widehat{A}=\widehat{H}=90^o\)
Do do : \(\Delta ABH~\Delta ABC\left(g-g\right)\)
=> \(\frac{AB}{HB}=\frac{BC}{AB}\) (tỉ lệ tương ứng của 2 tam giác đồng dạng )
=> AB . AB = BH . BC
=> AB2 = BH . BC
b)

A B C 6 8 H D I
a, Xét tam giác ABC vuông tại A, có AH là đường cao
Áp dụng định lí Py ta go ta có :
\(BC^2=AB^2+AC^2=36+64\)
\(\Rightarrow BC^2=100\Rightarrow BC=10\)cm
Vì BD là phân giác ^ABC nên
\(\frac{AB}{BC}=\frac{AD}{DC}\)(1) mà \(AD=AC-DC=8-DC\)
hay \(\frac{6}{10}=\frac{8-DC}{DC}\Rightarrow6DC=80-10DC\)
\(\Leftrightarrow16DC=80\Leftrightarrow DC=5\)cm
\(\Rightarrow AD=AC-DC=8-5=3\)cm
b, Xét tam giác BHA và tam giác BAC ta có
^BHA = ^A = 900
^B _ chung
Vậy tam giác BHA ~ tam giác BAC ( g.g )
\(\Rightarrow\frac{BH}{BA}=\frac{AB}{BC}\) ( tỉ số đồng dạng ) (2)
Từ (1) và (2) \(\Rightarrow\frac{BH}{BA}=\frac{AD}{DC}\)(3)
xem lại đề đi nếu như thành \(\frac{IH}{AD}=\frac{IA}{DC}\)
sao lại có tam giác IHA được ? hay còn cách nào khác ko ?