Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABD và tam giác EBD có :
AB= BE ( giả thiết ) (1)
Góc B1 = góc B2 ( vì tia BD là tia phân giác ) (2)
BD : cạnh chung (3)
Từ (1) ;(2) và (3) => tam giác ABD = tam giác EBD ( cạnh - góc - cạnh )
b) Vì tam giác ABD = tam giác EBD ( chứng minh ở câu a)
=> góc BAD = góc BED ( cặp góc tương ứng )
Mà góc BAD = 90 độ
=> BED = 90 độ
c) Vì góc BED = 90 độ
=> tam giác BED vuông
d) Vì AH vuông góc với BC ( giả thiết) (1)
và DE vuông góc với BC ( giả thiết ) (2)
Từ (1) và (2) => AH // DE ( điều phải chứng minh).

e) vì AC vuông góc vs BK , KE ( kéo dài ED)vuông góc với BC mà AC và KE cắt nhau tại D => D là trực tâm của tam giác KBC => BD vuoogn góc với KC ( 1 ) .M là trung điểm của KC => BM là đường cao đồng thời là đường trung trực của tam giác KBC ( 2 ) . từ ( 1 ) và ( 2 ) => B, D , M thằng hàng

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>DA=DE và góc BED=góc BAD=90 độ
b; AH vuông góc BC
DE vuông góc BC
=>AH//DE

Answer:
Phần c) thì nhờ các cao nhân khác thoii.
C E D A B 1 2
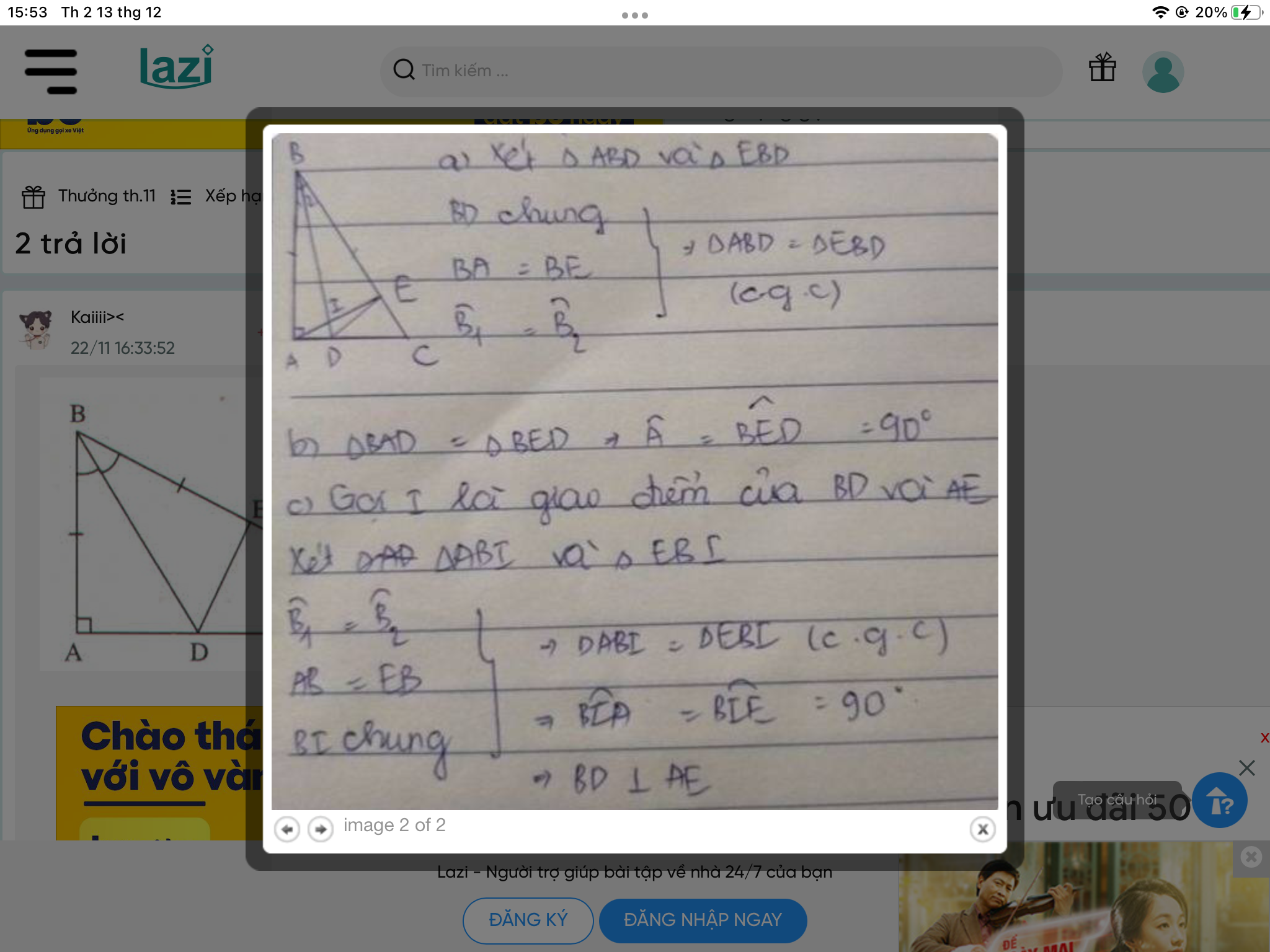
a) Ta xét tam giác ABD và tam giác EBD:
AB = EB (gt)
BD cạnh chung
\(\widehat{B_1}=\widehat{B_2}\)
Vậy tam giác ABD = tam giác EBD (c.g.c)
\(\Rightarrow DE=DA\)
b) Theo phần a), tam giác ABD = tam giác EBD
\(\Rightarrow\widehat{BAD}=\widehat{BED}=90^o\)

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD