
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



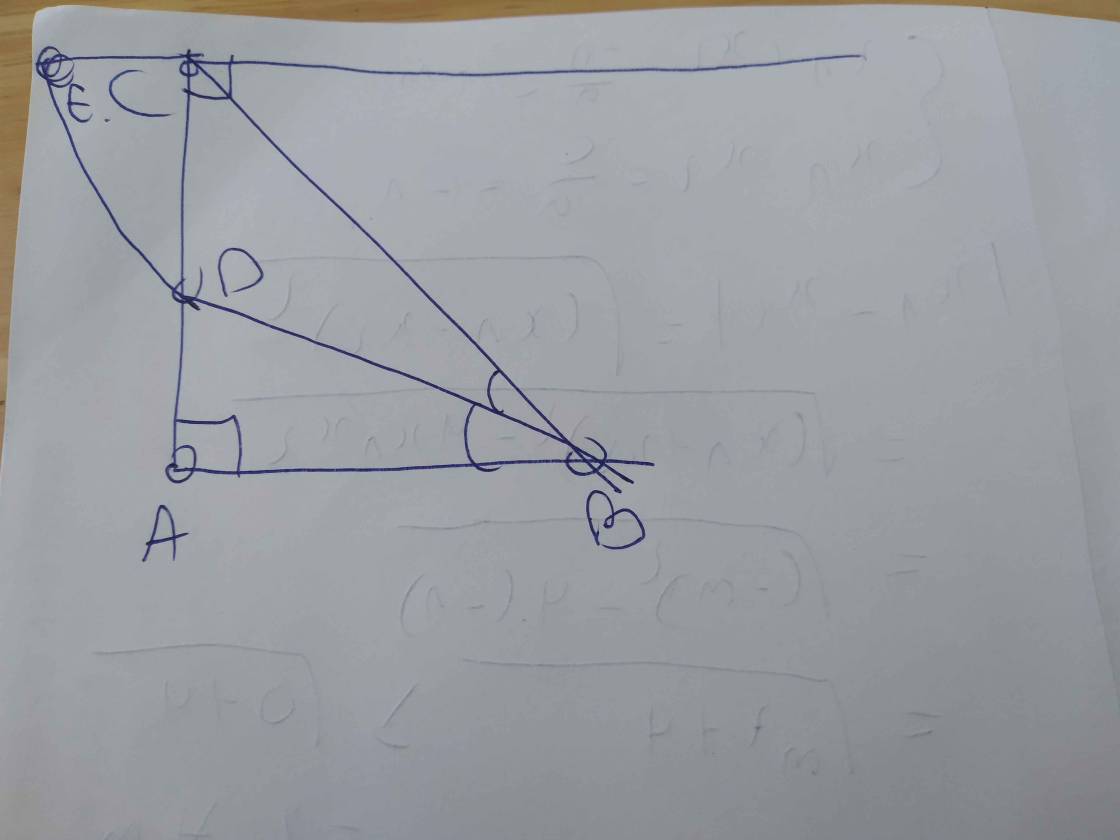
Bạn tự vẽ hình nha![]()
a.
Tam giác ABD vuông tại A có: ABD + ADB = 90
Tam giác CED vuông tại C có: CED + EDC = 90
mà ADB = EDC (2 góc đối đỉnh)
=> ABD = CED
mà ABD = CBD (BD là tia phân giác của ABC)
=> CED = CBD
=> Tam giác BEC cân tại C
b.
Tam giác ABC vuông tại A có:
BC > AB (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà BC = EC (tam giác BEC cân tại C)
=> EC > AB
=> DE > DB (quan hệ giữa đường xiên và hình chiếu)
c.
CA là đường cao của tam giác MBC
BD là đường cao của tam giác MBC
=> D là trực tâm của tam giác MBC
=> MD là đường cao của tam giác MBC
hay MD _I_ BC
Chúc bạn học tốt![]()

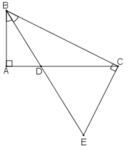
+) Ta có BD là tia phân giác của góc ABC nên: ∠(ABD) = ∠(DBC) (1)
+ Lại có: ∠(ADB)= ∠(CDE) ( hai góc đối đỉnh) (2)
+) Tam giác ABD vuông tại A nên:
∠ (ABD) + ∠(ADB) = 90° (tính chất tam giác vuông) (3)
Từ (1); (2) và (3) suy ra: ∠ (DBC) + ∠(CDE) = 90° (4)
+) Tam giác BCE vuông tại C nên:
∠ (DBC) + ∠(BEC) = 90° (tính chất tam giác vuông) (5)
Từ (4) và (5) suy ra : ∠ (CDE) = ∠(BEC)
Vậy tam giác CDE có hai góc bằng nhau.