Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B A C H N M
tam giác AHB vuông tại H có HM là trung tuyến ứng với cạnh huyền AB=> HM=1/2AB=>AB=2HM=2.15=30cm
tam giác AHC vuông tại H có HN là trung tuyến ứng với cạnh huyền AC=>HN=1/2AC=>AC=2HN=2.20=40 cm
tam giác ABC vuông tại A =>\(BC^2=AB^2+AC^2suyraBC=\sqrt{AB^2+AC^2}=\sqrt{30^2+40^2}=50cm\)
ta có AH.BC=AB.AC=>AH=[30.40]/50=24cm hệ thức lượng tam giác vuông
ta có \(AB^2=BH.BCsuyraBH=\frac{AB^2}{BC}=\frac{30^2}{50}=18cm\)
suy ra HC=BC-BH=50-18=32cm

A B C H M N
Vì M là trung điểm của AB => HM là trung tuyến
Mà \(\Delta ABH\)vuông tại H
=> \(HM=\frac{1}{2}AB\)( trong tam giác vuông trung tuyến ứng với cạnh huyền = 1 phần 2 cạnh huyền )
=> AB = 30 cm
Chứng minh tương tự
=> AC= 40 cm
Xét \(\Delta ABC\)có ( A = 900 )
=> \(BC=\sqrt{AC^2+AB^2}=50\)cm
Áp dụng hệ thức cạnh trong tam giác vuông ta có :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
\(\Rightarrow\frac{1}{AH}=\sqrt{\frac{1}{AB^2}+\frac{1}{AC^2}}=\frac{1}{24}\)
\(\Rightarrow AH=24cm\)
Áp dụng hệ thức cạnh trong tam giác vuông ta có :
\(AB^2=BH.BC\)
\(\Rightarrow BH=AB^2:BC=18cm\)
Vì BH + HC = BC
\(\Rightarrow HC=50-18=32cm\)
Study well

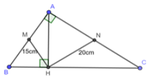
Xét ∆ ABC vuông tại A có M là trung điểm AB
=> HM là đường trung tuyến ứng với cạnh huyền AB
=> HM = 1 2 AB => AB = 2HM = 2. 15 = 30 (cm)
Xét ∆ ACH vuông tại H có N là trung điểm AC
=> HN là đường trung tuyến ứng với cạnh huyền AC
=> HN = 1 2 AC => AC = 2HN = 2. 20 = 40 (cm)
Áp dụng định lý Pitago cho ABH vuông tại A có:
![]()
![]()
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
![]()
Ta có: HC = BC – BH = 50 – 18 = 32 (cm)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
AH.BC = AB.AC => AH.50 = 30.40 => AH = 24 (cm)
Đáp án cần chọn là: D

Nối M với N .
Dùng công thức đường trung bình của hình tam giác , ta có :
NM // BC và NM = \(\dfrac{1}{2}\) BC
Cm : Tam giác MNH vuông , dùng định lí pytago ta suy ra được MN=25 và BC=50 (vì MN = \(\dfrac{1}{2}\) BC)
Từ đây ta suy ra được BA=40 và AC=30
Vì tam giác ABC vuông nên ta có công thức : BA . AC = BC . AH
40 . 30 = 50 . AH
Ta suy ra : AH = 24
Tam giác ABH vuông tại A , ta dùng định lí pytago suy ra HB=32 và HC=18 ( HC + BH = BC = 50 )
Suy ra BH = 32 ; CH = 18 ; AH = 24

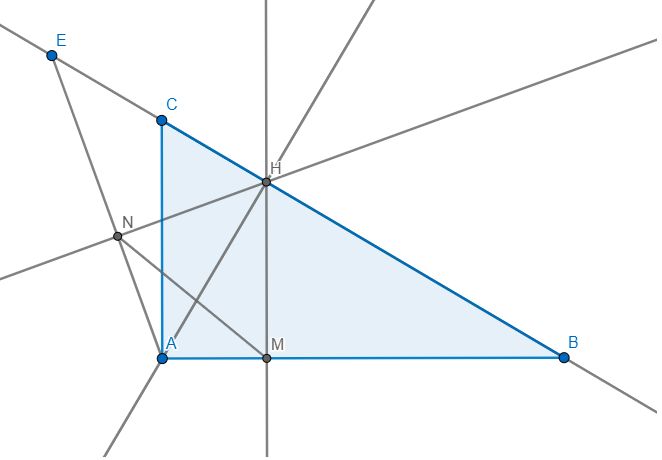
c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

a: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
XétΔABC vuông tại A có \(\sin C=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
=>\(\widehat{B}\simeq53^0\)
b: \(AH=\dfrac{AB\cdot AC}{BC}=2.4\left(cm\right)\)
\(HB=\dfrac{BA^2}{BC}=\dfrac{3^2}{5}=1.8\left(cm\right)\)
HC=BC-HB=3,2(cm)
c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔHCA vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
d: Xét tứgiác AMHN có \(\widehat{AMH}+\widehat{ANH}=180^0\)
nên AMHN là tứ giác nội tiếp
Xét (AH/2) có
\(\widehat{ANM}\) là góc nội tiếp chắn cung AM
\(\widehat{AHM}\) là góc nội tiếp chắn cung AM
DO đó: \(\widehat{ANM}=\widehat{AHM}=\widehat{B}\)
Ta có: ΔABC vuông tại A
mà AE là đường trung tuyến
nên AE=CE
=>\(\widehat{EAC}=\widehat{C}\)
\(\widehat{ANM}+\widehat{EAC}=\widehat{B}+\widehat{C}=90^0\)
=>AE\(\perp\)MN

tự vẽ hình nha bn
a. Ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\)(Theo định lí Pytago, tam giác ABC vuông tại A)
b. Ta có: \(\frac{BH}{CH}=\frac{3}{4}\)
\(\Leftrightarrow\frac{BH+CH}{CH}=\frac{3}{4}+1\)
\(\Leftrightarrow\frac{BC}{CH}=\frac{7}{4}\)\(\Leftrightarrow\frac{5}{CH}=\frac{7}{4}\)\(\Leftrightarrow CH=\frac{5.4}{7}=\frac{20}{7}\)
\(\Rightarrow BH=5-\frac{20}{7}=\frac{15}{7}\)

Xét tg ABH vuông tại H có Ma=MB=> MH là đường trung tuyến
=>MH=\(\frac{1}{2}\)AB=>AB=30cm
Xét tg AHC vuông tại H có AN=NC=>HN là đường trung tuyến
=>HN=\(\frac{1}{2}\)AC=>AC=40cm
Xét tg ABC vuông tại A có:
BC2=AB2+AC2(py-ta-go)
=>BC=50cm
Xét tg ABC có góc A=90o,đg cao AH ứng vs cạnh huyền BC.Aps dụng HTL tro tg vuông ta có:
AB2=BC.BH=>BH=18cm
Lại có:AC2=HC.BC=>HC=32cm
AH2=BH.HC =>AH=24cm

a) Ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{16^2+12^2}=20\left(cm\right)\)
Ta có: \(AB.AC=AH.BC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12.16}{20}=\dfrac{48}{5}\left(cm\right)\)
Ta có: \(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{16^2}{20}=\dfrac{64}{5}\left(cm\right)\)
Ta có: \(sinB=\dfrac{AC}{BC}=\dfrac{12}{20}=\dfrac{3}{5}\Rightarrow\angle B\approx37\)
b) tam giác AHE vuông tại H có HN là đường cao \(\Rightarrow AN.AE=AH^2\)
tam giác ABC vuông tại A có AH là đường cao \(\Rightarrow AH^2=HB.HC\)
\(\Rightarrow AN.AE=HB.HC\)
c) tam giác AHB vuông tại H có HM là đường cao \(\Rightarrow AH^2=AM.AB\)
\(\Rightarrow AN.AE=AM.AB\Rightarrow\dfrac{AM}{AE}=\dfrac{AN}{AB}\)
Xét \(\Delta AMN\) và \(\Delta AEB:\) Ta có: \(\left\{{}\begin{matrix}\angle EABchung\\\dfrac{AM}{AE}=\dfrac{AN}{AB}\end{matrix}\right.\)
\(\Rightarrow\Delta AMN\sim\Delta AEB\left(c-g-c\right)\Rightarrow\dfrac{AE}{AM}=\dfrac{BE}{MN}\)
mà \(BE=3MN\Rightarrow\dfrac{BE}{MN}=3\Rightarrow\dfrac{AE}{AM}=3\Rightarrow AE=3AM\)