Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(hình bạn tự kẻ nhé)
a) \(\Delta\)ABC : BAC^ = 90o ;BCA^ = 30o => ABC^ = 180o - BAC^ -BCA^ = 180o - 90o - 30o = 60o
\(\Delta\)BHA : BHA^ = 90o ; HBA^ = 60o => BAH^ = 180o - BHA^ - HBA^ = 180o - 90o - 60o = 30o
Xét \(\Delta\)BHA và \(\Delta\)DHA :
BHA^ = DHB^ = 90o
HA chung
HB = HD
=> \(\Delta\)BHA = \(\Delta\)DHA (2 cạnh góc vuông)
=> BAH^ = DAH^ = 30o (2 cạnh tương ứng)
Ta có: BAH^ + DAH^ = BAD^ <=> 30o + 30o = BAD^ => 60o = BAD^
\(\Delta\)ABD có: ABD^ = 60o; BAD^ = 60o
Và ABD^ + BAD^ + BDA^ = 180o
BDA^ = 180o - ABD^ - BAD^ = 180o - 60o - 60o = 60o
=> \(\Delta\)ABD đều
b) Ta có: \(\Delta\)BHA = \(\Delta\)DHA (cmt)
=> AH = CE (2 cạnh tương ứng)
c) Ta có: HDE^ = ADC^ (đđ)
và HDA^ = EDC^ = 60o (đđ)
mà HDE^ + ADC^ + HDA^ + EDC^ = 360o
2 * HDE^ + 2* HDA^ = 360o
2* HDE^ + 2* 60o = 360o
2* HDE^ = 360o - 120o
2* HDE^ = 240o
HDE^ = 120o
\(\Delta\)BHA = \(\Delta\)DHA (cmt)
=> DH = DE (2 cạnh tương ứng)
=> \(\Delta\)HDE cân tại D
=> DHE^ = DEH^
\(\Delta\)HDE có: DHE^ + DEH^ + HDE^ = 180o
2* DHE^ = 180o - HDE^ = 180o - 120o = 60o
DHE^ = 30o
=> DHE^ = DCA^ = 30o
Mà DHE^ sole trong với DCA^
=> EH // AC
a) ΔABDΔABD có đường cao AH đồng thời là đường trung tuyến nên ABDABD cân.
Có ˆB=600B^=600 (vì ˆC=300C^=300 (gt)).
Do đó ΔABDΔABD đều.
b) ΔABDΔABD đều (cmt) ⇒ˆBAD=600⇒ˆCAD=ˆC=300.⇒BAD^=600⇒CAD^=C^=300.
Do đó ΔADCΔADC cân tại D ⇒DA=DC.⇒DA=DC.
Xét hai tam giác vuông AHD và CED có:
+) DA=DCDA=DC (cmt);
+) ˆD1=ˆD2D^1=D^2 (đđ);
Vậy ΔAHD=ΔCEDΔAHD=ΔCED (cạnh huyền-góc nhọn)
⇒AH=CE.⇒AH=CE.
c) ΔAHD=ΔCEDΔAHD=ΔCED(cmt) ⇒HD=ED⇒HD=ED (cạnh tương ứng).
Do đó ΔDHEΔDHE cân tại D.
Mặt khác ΔADCΔADC cân tại D, mà hai tam giác cân này chung đỉnh D
⇒ˆCHE=ˆACB=300.⇒CHE^=ACB^=300.
⇒⇒ EH // AC (cặp góc so le trong bằng nhau).

a) trong tam giác ABC có: Â + B + C = 1800 (đ/lý)
=> 900 + B + 300 = 1800
=> B = 1800 - (900 + 300)
B = 600 (1)
xét 2 tam giác vuông ABH và ADH có:
AH chung
HD = HB (gt)
=> tam giác ABH = tam giác ADH (ch-cgv)
=> AB = AD (cạnh tương ứng)
=> tam giác ABD cân tại A (2)
từ (1) và (2) => tam giác ABD là tam giác đều

a) xét tam giác ABD có AH là đường cao( AH vuông góc với BC)
đồng thời AH là đường trung tuyến( HD=HB)
=> tam giác ABD cân tại A(1)
lại có tam gisc ABC vuông tại A, gocs C=30 độ
=> góc B=90 độ = 90-30 =60 độ(2)
từ(1) (2)=> tam giác ABD đều
b) tam giác ABD đều => góc BAD=60 độ
vậy ta có góc BAD+góc DAC=90
hay 60+góc DAC=90
góc DAC=30 độ
Xét tam giác ADC có góc DAC=góc DCA=30
Vậy tam giác ADC cân tại D=> AD=DC
Xét tam giác ADH và tam giác CDE có
góc DEC=góc DHA=90
AD=CD(cmt)
góc CDE=góc ADH(đối đỉnh)
=> tam giác ADH=tam giác CDE(ch-gc)
=> AH= CE(2 cạnh tương ứng)
a, xét tam giác ABD có AH là đường cao( AH vuông góc với BC)
đồng thời AH là đường trung tuyến( HD=HB)
=> tam giác ABD cân tại A(1)
lại có tam gisc ABC vuông tại A, godc C=30 độ
=> góc B=90 độ-gócc
=90-30 =60 độ(2)
từ(1) (2)=> tam giác ABD đều

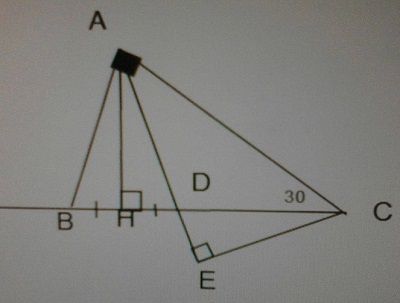
A B C H E D
Mk vẽ hình ko đc đẹp bạn vẽ lại nha
Tam giác ABC có BAC+ABC+ACB=180
90+30+ABC=180
=> ABC= 60
=> Tam giác Abc là tam giác đều
b,Xét tam giác ADH và Tam giác ABH
AH chung; BH= DH; AHD=AHB
=> tam giác ADH=tam giác AHB (c.g.c)
=>ABH=ADH=60=> tam giác BAD đều => BAD=60
ta có BAD+CAD=90 => CAD=30
Tam giác có CAD=DCA=30 => tam giác CAD cân tại D=> DA=DC
Xét tam giác ADH và tam giác CDE
DA=DC; DEC=ADH=90
=> =(ch-gn)=> AH=CE


a) Áp dụng tính chất tổng ba góc ta có :
A + B + C = 180 độ
90 độ + B + 30 độ = 180 độ
B = 60 độ
Xét tam giác AHB và tam giác ADH, có:
AH là góc chung
=> AHB = AHD = 90 độ
=> HB = HD (gt)
Vậy ADH = ABH (c.g.c)
=> AB = AD (có 2 cạnh tương ứng)
=> Tam giác ABD là tam giác đèu
b) ABD đều => BAD = 60 độ
Vậy BAD + DAC = 90 độ
=> 60 độ + DAC = 90 độ
=> DAC = 30 độ
Xét từng tam giác ta có :
Tam giác DAC có góc DAC = 30 độ
Vậy tam giác DAC cận tại D
=> AD = CD
Xét 2 tam giác ADH và CDE có DEC = DEH = 90 độ
=> AD = CD
=> CED = AHD
=> EHD = CED (ch - gc)
=> AH = CE
c) DE = DH (cạnh tương ứng)
Vậy DHE cân tại E.
=> DHE = (180 - EHD) : 2 => cân tại D
=> DAC = (180 - ADC) : 2 => ADC = EDH (đối đỉnh)
=> DEH = DAC
Mà DEH = DAC so le trong.
Vậy EH//AC