Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

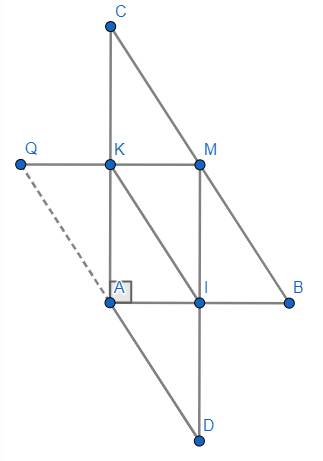
(a) \(I,M\) là trung điểm của \(AB,BC\Rightarrow IM\) là đường trung bình của \(\Delta ABC\Rightarrow\left\{{}\begin{matrix}IM\left|\right|AC\Leftrightarrow MD\left|\right|AC\left(1\right)\\IM=\dfrac{1}{2}AC\end{matrix}\right.\)
Lại có: \(IM=ID\Rightarrow MD=2IM=2\cdot\dfrac{1}{2}AC=AC\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\Rightarrow ADMC\) là hình bình hành (điều phải chứng minh).
(b) \(\left\{{}\begin{matrix}MI\left|\right|AC\left(cmt\right)\\AC\perp AB\left(gt\right)\end{matrix}\right.\Rightarrow MI\perp AB\Rightarrow\hat{AIM}=90^o\left(3\right)\).
\(M,K\) là trung điểm của \(BC,AC\Rightarrow MK\) là đường trung bình của \(\Delta ABC\Rightarrow MK\left|\right|AB\), mà \(AB\perp AC\left(gt\right)\Rightarrow MK\perp AC\Rightarrow\hat{AKM}=90^o\left(4\right)\).
Ta cũng có: \(\hat{A}=90^o\left(5\right)\).
Từ \(\left(3\right),\left(4\right),\left(5\right)\Rightarrow AIMK\) là hình chữ nhật (điều phải chứng minh).
(c) Do \(AIMK\) là hình chữ nhật (chứng minh trên) nên \(\left\{{}\begin{matrix}AK\left|\right|MI\Leftrightarrow AK\left|\right|ID\\AK=MI=ID\end{matrix}\right.\Rightarrow AKID\) là hình bình hành \(\Rightarrow IK\left|\right|AD\left(6\right)\).
Lại có: \(I,K\) là trung điểm của \(MD,MQ\Rightarrow IK\) là đường trung bình của \(\Delta MQD\Rightarrow IK\left|\right|QD\left(7\right)\)
Từ \(\left(6\right),\left(7\right)\Rightarrow Q,A,D\) thẳng hàng (điều phải chứng minh).

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

a) Xét tứ giác AMIN có:
∠(MAN) = ∠(ANI) = ∠(IMA) = 90o
⇒ Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).
b) ΔABC vuông có AI là trung tuyến nên AI = IC = BC/2
do đó ΔAIC cân có đường cao IN đồng thời là đường trung tuyến
⇒ NA = NC.
Mặt khác ND = NI (t/c đối xứng) nên ADCI là hình bình hành
Lại có AC ⊥ ID (gt). Do đó ADCI là hình thoi.
c) Ta có: AB2 = BC2 – AC2 (định lí Py-ta-go)
= 252 – 202 ⇒ AB = √225 = 15 (cm)
Vậy SABC = (1/2).AB.AC = (1/2).15.20 = 150 (cm2)
d) Kẻ IH // BK ta có IH là đường trung bình của ΔBKC
⇒ H là trung điểm của CK hay KH = HC (1)
Xét ΔDIH có N là trung điểm của DI, NK // IH (BK // IH)
Do đó K là trung điểm của DH hay DK = KH (2)
Từ (1) và (2) ⇒ DK = KH = HC ⇒ DK/DC= 1/3.