Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

| GT | Tam giác ABC, góc A=90o, góc ABD = góc MBD, BM = BA |
| KL | DM vuông góc với BC |
- Xét \(\Delta ABD\) và \(\Delta MBD\) ta có:
BD là cạnh chung
góc ABD = góc MBD
BA = BM ( gt )
=> \(\Delta ABD=\Delta MBD\) ( Trường hợp c-g-c )
=> góc A = góc BMD ( Cặp góc tương ứng )
Góc A = 90o => góc BMD = 90o
<=> DM vuống góc với BC.

Tham khảo:
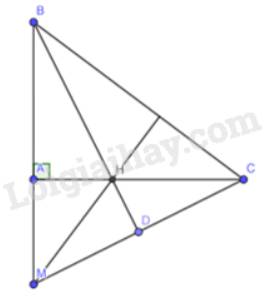
Gọi D giao điểm của tia phân giác của góc B và MC
Xét tam giác BDM và tam giác BDC có :
BD chung
\(\widehat {MBD} = \widehat {CBD}\) ( BD là phân giác của góc B)
BM = BC ( giả thiết )
( \Rightarrow \Delta BDM=\Delta BDC\)(c.g.c)
\( \Rightarrow \widehat {BDM} = \widehat {BDC}\)(2 góc tương ứng)
Mà 2 góc ở vị trí kề bù \( \Rightarrow \widehat {BDM} = \widehat {BDC} = {90^o} \Rightarrow BD \bot CM\)
Mà AC cắt BD tại H \( \Rightarrow \) H là trực tâm tam giác BMC
\( \Rightarrow \) MH là đường cao của tam giác BMC (định lí 3 đường cao đi qua trực tâm tam giác)
\( \Rightarrow \) MH vuông góc với BC

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ACB}=90^0-\widehat{ABC}\)
\(\Leftrightarrow\widehat{ACB}=90^0-60^0\)
hay \(\widehat{ACB}=30^0\)
Vậy: \(\widehat{ACB}=30^0\)
b) Xét ΔADB và ΔEDB có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔADB=ΔEDB(c-g-c)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
hay DE\(\perp\)BC(đpcm)
c) Ta có: BE+EC=BC(E nằm giữa B và C)
BA+AM=BM(A nằm giữa B và M)
mà BE=BA(ΔBED=ΔBAD)
và BC=BM(gt)
nên EC=AM
Xét ΔADM vuông tại A và ΔEDC vuông tại E có
DA=DE(ΔDAB=ΔDEB)
AM=EC(cmt)
Do đó: ΔADM=ΔEDC(hai cạnh góc vuông)
nên \(\widehat{ADM}=\widehat{EDC}\)(hai góc tương ứng)
mà \(\widehat{EDC}+\widehat{ADE}=180^0\)(hai góc kề bù)
nên \(\widehat{ADM}+\widehat{ADE}=180^0\)
\(\Leftrightarrow\widehat{EDM}=180^0\)
hay E,D,M thẳng hàng(đpcm)

a) Xét ΔAMB và ΔEMB có
BA=BE(gt)
\(\widehat{ABM}=\widehat{EBM}\)(BM là tia phân giác của \(\widehat{ABE}\))
BM chung
Do đó: ΔAMB=ΔEMB(c-g-c)
Suy ra: \(\widehat{MAB}=\widehat{MEB}\)(hai góc tương ứng)
mà \(\widehat{MAB}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{MEB}=90^0\)
hay ME\(\perp\)BC(đpcm)
b) Ta có: ΔABC vuông tại A(gt)
\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ABC}+30^0=90^0\)
\(\Leftrightarrow\widehat{ABC}=60^0\)
hay \(\widehat{ABE}=60^0\)
Xét ΔABE có BA=BE(gt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
Xét ΔBAE cân tại B có \(\widehat{ABE}=60^0\)(cmt)
nên ΔBAE đều(Dấu hiệu nhận biết tam giác đều)

xét tam giác ABD và BDM
ABD=DBM (tia BD là tia p.giác của ABM)
BD là cạnh chung
BA=BM (gt)
vậy tan giác ABD=BDM
\(\Rightarrow BAD=BMD\)=90
vậy DM vuông góc với BC
Ta có hình vẽ:
B C D A M
Vì tia phân giác góc B cắt AC tại D nên \(ABD=DBM=\frac{ABM}{2}\)
Xét Δ ABD và Δ MBD có:
AB = BM (gt)
ABD = DBM (chứng minh trên)
BD là cạnh chung
Do đó, Δ ABD = Δ MBD (c.g.c)
=> BAD = BMD = 90o (2 góc tương ứng)
=> \(DM\perp BM\) hay \(DM\perp BC\left(đpcm\right)\)
cảm ơn nha
mk chờ bn mãi