Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C E D I
a) Xét tam giác ABD và EBD có:
BA = BE (gt)
\(\widehat{ABD}=\widehat{EBD}\) (Do BD là tia phân giác góc B)
BD chung
\(\Rightarrow\Delta ABD=\Delta EBD\left(c-g-c\right)\)
\(\Rightarrow AD=ED\) (Hai cạnh tương ứng)
b) Do \(\Delta ABD=\Delta EBD\left(cmt\right)\Rightarrow\widehat{BED}=\widehat{BAD}=90^o\)
Xét tam giác vuông ABC ta có \(\widehat{ABC}=90^o-\widehat{ACB}\)
Xét tam giác vuông DEC ta có \(\widehat{EDC}=90^o-\widehat{ACB}\)
Vậy nên \(\widehat{EDC}=\widehat{ABC}\)
c) Gọi giao điểm của AE và BD là I.
Xét tam giác ABI và tam giác EBI có:
AB = EB (gt)
\(\widehat{ABI}=\widehat{EBI}\)
BD chung
\(\Rightarrow\Delta ABI=\Delta EBI\left(c-g-c\right)\)
\(\Rightarrow\widehat{AIB}=\widehat{EIB}\) (Hai góc tương ứng)
Mà chúng lại ở vị trí kề bù nên \(\widehat{AIB}=\widehat{EIB}=90^o\)
Vậy nên \(AE\perp BD\)

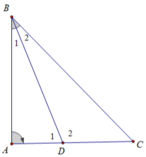
Cách 1. Xét tam giác ABD có ∠D2 là góc ngoài tam giác tại đỉnh D nên:
∠D2 = ∠B1 + ∠A
Suy ra: ∠D2 > ∠A (góc ngoài của ΔABD)
mà ∠A = 90o nên ∠D2 > 90o.
ΔBDC có ∠D2 > 90o nên ∠D2 > ∠C , do đó BC > BD.
Cách 2. Xét các đường xiên BD, BC.
Đoạn thẳng AD; AC lần lượt là hình chiếu của BD; BC trên đường thẳng AC.
Hình chiếu AC > AD nên đường xiên BC > BD. ( quan hệ đường xiên và hình chiếu của chúng ).

a: ΔABD vuông tại A
=>BA<BD
b: Xét ΔCAE vuông tại A và ΔCAB vuông tại A có
CA chung
AE=AB
=>ΔCAE=ΔCAB
c: BA<BC
=>AD<CD

a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
=>DA=DH
b: AD=DH
DH<DC
=>AD<DC
c: Xét ΔBKC có
KH,CA là đường cao
KH cắt CA tại D
=>D là trực tâm
=>BD vuông góc KC

AD>AB
Áp dụng bài hình chiếu của tam giác vuông ấy bạn,hình như thế

a) Xét tam giác ACE và tam giác AKE
có AE chung
góc CAE =góc KAE (GT)
góc ECA = góc EKA =900
suy ra tam giác ACE = tam giác AKE (cạnh huyền-góc nhọn) (1)
b) Từ (1) suy ra AC=AK suy ra A thuộc đường trung trực của CK (2)
Từ (1) suy ra EK=EC suy ra E thuộc đường trung trực của CK (3)
Từ(2) và (3) suy ra AE là đường trung trực của CK
c) tam giác ABC vuông tại C, có góc CAB = 600
suy ra AC=AB:2 ( cạnh đối diện với góc 30 độ bằng nửa cạnh huyền)
mà AK=AC , AK +KB=AB
suy ra AK=AC=KB
d) tam giác BDE=tam giác BKE (cạnh huyền-góc nhọn)
(Câu này mình tìm thấy của Lê Thị Nhung ở h https://h.vn/vip/lethinhung262)
+) Xét tam giác BDC có ∠D1 là góc ngoài tam giác tại đỉnh D nên:
∠D1 = ∠B2 + ∠C
Suy ra: ∠D1 > ∠B2 (góc ngoài của ΔBDC)
Mà ∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC ) nên ∠D1 > ∠B1 .
ΔABD có ∠D1 > ∠B1 nên AB > AD.