Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề bài không đúng.
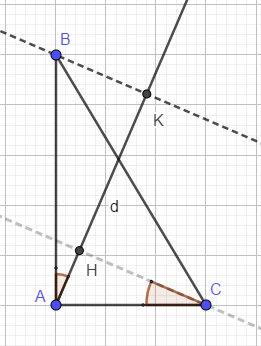
Đặt \(\alpha=\widehat{HCA};AB=c;AC=b\) thì \(\widehat{BAH=\alpha}\) và \(KB=c\sin\alpha;HC=b\cos\alpha\) từ đó
\(KB^2+HC^2=c^2\sin^2\alpha+b^2\cos^2\alpha\)
Nếu \(\alpha=45^0\)thì \(KB^2+HC^2=c^2\sin^245^0+b^2\cos^245^0=\frac{1}{2}\left(c^2+b^2\right)\).
Nếu \(\alpha=30^0\) thì \(KB^2+HC^2=c^2\sin^230^0+b^2\cos^230^0=\frac{1}{4}\left(c^2+3b^2\right)\).
Nếu \(\alpha=60^0\) thì \(KB^2+HC^2=c^2\sin^260^0+b^2\cos^260^0=\frac{1}{4}\left(3c^2+b^2\right)\).
Như vậy tổng \(KB^2+HC^2\) thay đổi khi đường thẳng d quay quanh A.

Qua A kẻ đường thẳng vuông góc với d, cắt BC tại D
Ta có BH,CK,DA cùng vuông góc d nên các đường thẳng này song song nhau
Suy ra được các cặp góc bằng nhau là ACK=DAC, HBA=BAD
Tam giác ABC vuông tại A nên góc BAD+DAC=90 độ
nên ta có góc HBA+ góc ACK= 90 độ (1)
Tam giác AKC vuông tại K nên góc ACK+KAC= 90 độ (2)
Từ 1 và 2 ta có góc HBA= góc KAC
Xét 2 tam giác vuông HBA và KAC có cạnh huyền AB=AC, góc HBA= góc KAC
Nên 2 tam giác này bằng nhau suy ra HB=AK, HA=CK
Do đó HB^2+CK^2=HB^2+HA^2=AB^2