Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H M I K
Không mất tính tổng quát, ta xét M thuộc HC (trường hợp M thuộc HB tương tự)
Tam giác ABC vuông tại A có đường cao AH xuất phát từ đỉnh A nên \(AH=\frac{1}{2}BC\) (1) và AH cũng là đường trung tuyến \(\Rightarrow HC=HB=\frac{1}{2}BC\) (2) và đường phân giác => ^CAH = ^BAH. Từ (1) và (2) suy ra \(\Delta\)AHC vuông cân tại H. Từ đó
AH = HC và ^ACH = ^HAC = ^BAH. Tới đây tìm cách chứng minh AI = CK(mình chưa biết làm đâu:v). Từ đó suy ra \(\Delta\)HIA = \(\Delta\)HKC. Suy ra ^AHI = ^CHK suy ra ^IHK = ^IHA + ^AHK = ^CHK + ^AHK = 90o => \(\Delta\)IHK vuông tại H (3)
Mặt khác từ \(\Delta\)HIA = \(\Delta\)HKC suy ra HI =HK suy ra \(\Delta\)IHK cân tại H (4)
Từ (3) và (4) suy ra đpcm.
P/s: Ko chắc, bác zZz Cool Kid zZz check giúp:v

a: Xét tứ giác AIDK có
góc AID=góc AKD=góc KAI=90 độ
nên AIDK là hình chữ nhật
b: Vì AIDK là hình chữ nhật
nên AD cắt KI tại trung điểm của mỗi đường và AD=KI
=>ΔOAK cân tại O

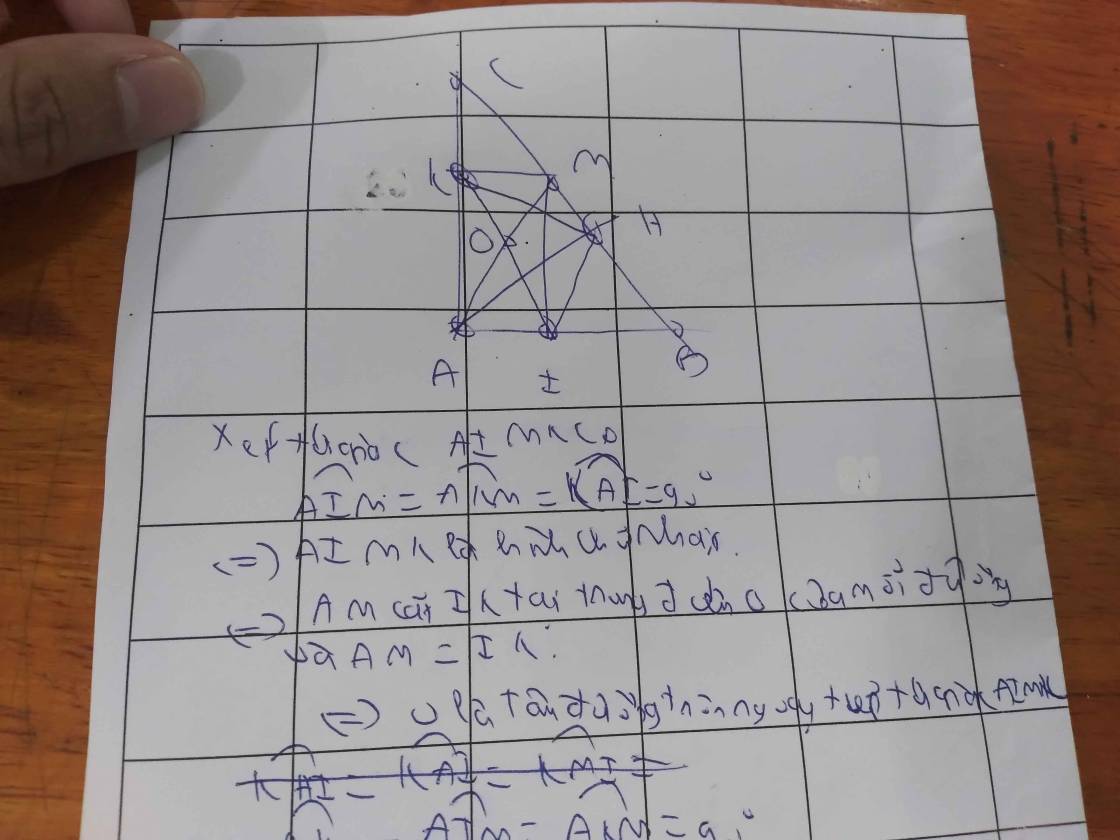
Xét tứ giác AIMK có
\(\widehat{AIM}=\widehat{AKM}=\widehat{KAI}=90^0\)
=>AIMK là hình chữ nhật
=>AIMK nội tiếp đường tròn đường kính AM và IK
=>Tâm O của đường tròn ngoại tiếp tứ giác AIMK là trung điểm chung của AM và IK
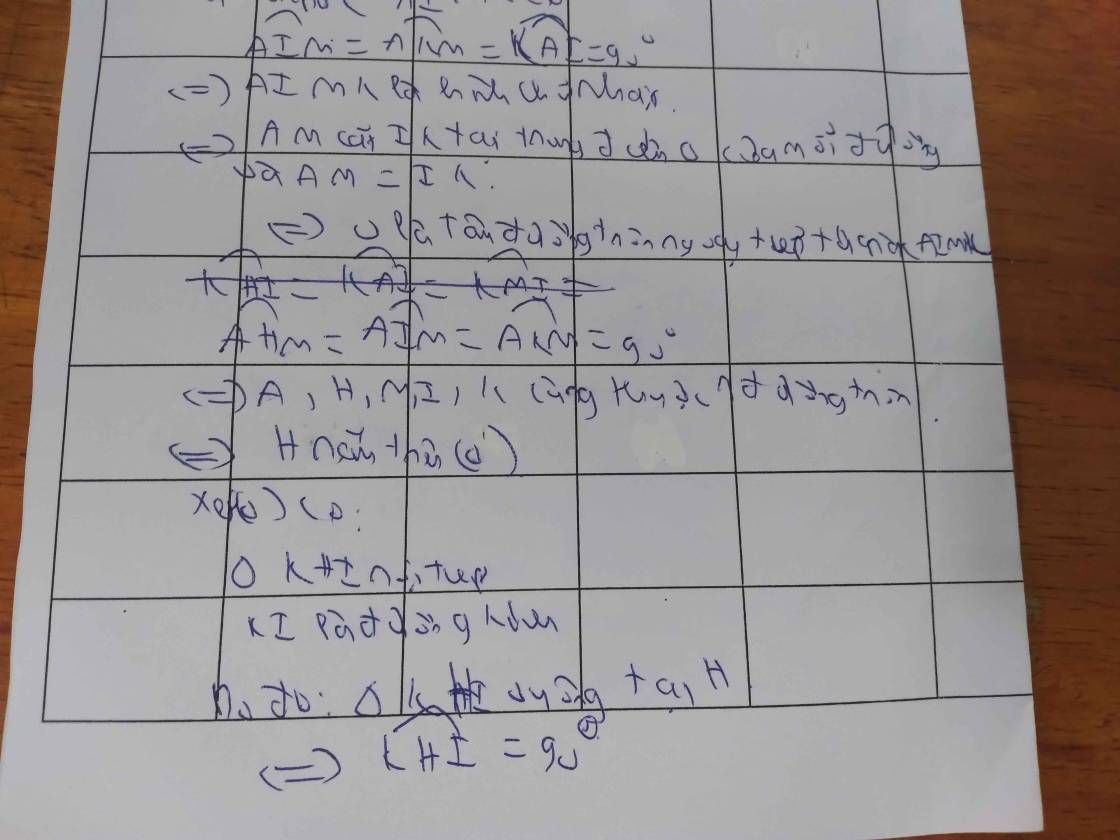
\(\widehat{AHM}=\widehat{AKM}=\widehat{AIM}=90^0\)
=>A,K,M,H,I cùng thuộc đường tròn đường kính AM
=>H thuộc (O)
Xét (O) có
ΔKHI nội tiếp
KI là đường kính
Do đó: ΔKHI vuông tại H
=>\(\widehat{KHI}=90^0\)