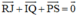Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

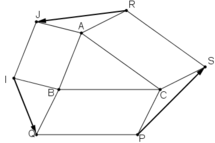
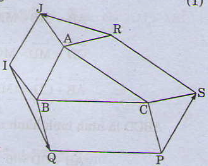
Ta có:
AJIB là hình bình hành nên 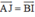
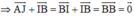
Tương tự như vậy:
BCPQ là hình bình hành nên 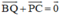
CARS là hình bình hành nên 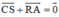
Do đó:


\(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \left( {\overrightarrow {RA} + \overrightarrow {AJ} } \right) + \left( {\overrightarrow {IB} + \overrightarrow {BQ} } \right) + \left( {\overrightarrow {PC} + \overrightarrow {CS} } \right)\)
\( = \left( {\overrightarrow {RA} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {AJ} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {BQ} + \overrightarrow {PC} } \right) = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)\(\)(đpcm)
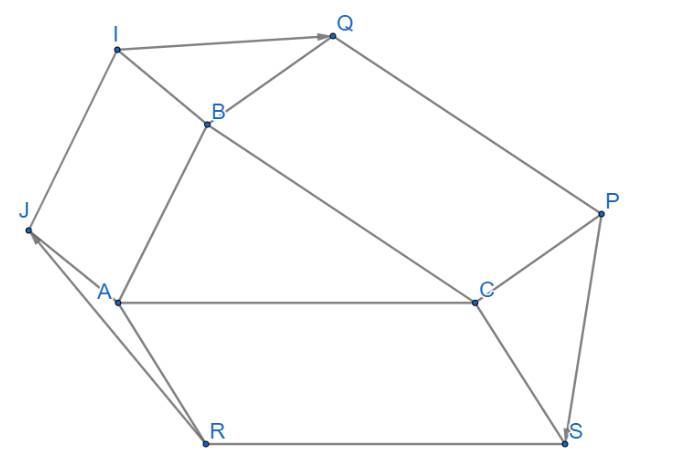

A B C I J R S P Q
Có \(\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{RA}+\overrightarrow{AJ}+\overrightarrow{IB}+\overrightarrow{BQ}+\overrightarrow{PC}+\overrightarrow{CS}\)
\(=\left(\overrightarrow{RA}+\overrightarrow{CS}\right)+\left(\overrightarrow{AJ}+\overrightarrow{IB}\right)+\left(\overrightarrow{BQ}+\overrightarrow{PC}\right)\)
\(=\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\). ( Do tứ giác ABIJ, BCPQ, CARS là hình bình hành).
Vậy \(\overrightarrow{RJ}+\overrightarrow{IQ}+\overrightarrow{PS}=\overrightarrow{0}\).

Tọa độ G là;
\(\left\{{}\begin{matrix}x=\dfrac{4+2+0}{3}=2\\y=\dfrac{0-4-2}{3}=-2\end{matrix}\right.\)
Tọa độ M là:
x=(2+0)/2=1 và y=(-4-2)/2=-3
Tọa độ N là:
x=(4+0)/2=2 và y=(0-2)/2=-1
Tọa độ P là;
x=(4+2)/2=3 và y=(0-4)/2=-2
Tọa độ trọng tâm của tam giác MNP là:
\(\left\{{}\begin{matrix}x=\dfrac{1+2+3}{3}=2\\y=\dfrac{-3-1-2}{3}=-2\end{matrix}\right.\)
=>Tam giác ABC và tam giác MNP có chung trọng tâm