Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tam giác ABC có góc B bằng 30 độ.Dựng phía ngoài tam giác ACD đều. Chứng minh \(BD^2=AB^2+BC^2\)


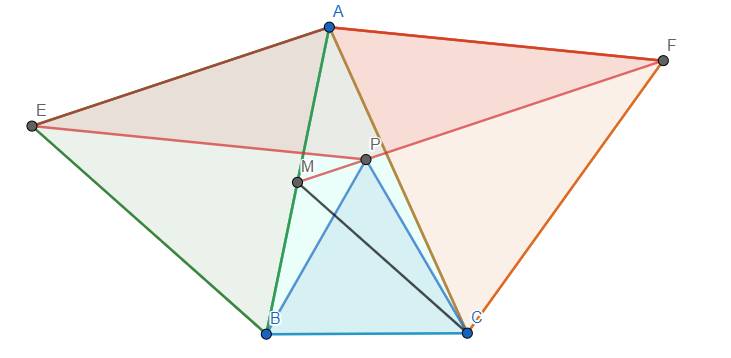
Gọi M là giao điểm của PE với AB.
Ta thấy rằng \(CF=AF=PE,PF=AE=EB\)
Đồng thời \(\widehat{BEP}=60^o-\widehat{AEP}=60^o-\widehat{AFP}=\widehat{PFC}\)
Dẫn đến \(\Delta PBE=\Delta CPF\left(c.g.c\right)\)
\(\Rightarrow PB=PC\) (1)
Mặt khác, \(\widehat{AMF}=\widehat{MAE}=60^o=\widehat{ACF}\) nên tứ giác AMCF nội tiếp.
\(\Rightarrow\widehat{BAC}=\widehat{PFC}\). Mà lại có \(AB=PF,AC=FC\) nên suy ra \(\Delta ABC=\Delta FPC\left(c.g.c\right)\)
\(\Rightarrow PC=BC\) (2)
Từ (1) và (2) \(\Rightarrow\Delta PBC\) đều (đpcm)


A B C D E F H I G K
Trên nửa mặt phẳng bờ BC có chứa điểm A, dựng \(\Delta\)BHC vuông cân tại H. Gọi giao điểm của AH và DF là I; HE giao BC tại G. Dựng điểm K đối xứng với F qua G.
Ta có: ^HBC = ^DBA (=450) => ^HBC + ^ABH = ^DBA + ^ABH => ^ABC = ^DBH (1)
\(\Delta\)ADB ~ \(\Delta\)CHB (Cùng là tam giác vuông cân) => \(\frac{AB}{CB}=\frac{BD}{BH}\)=> \(\frac{AB}{BD}=\frac{BC}{BH}\)(2)
Từ (1) và (2) => \(\Delta\)ABC ~ \(\Delta\)DBH (c.g.c) => \(\frac{AC}{DH}=\frac{AB}{DB}\)
Mà \(\frac{AB}{DB}=\frac{AC}{AF}\) nên \(\frac{AC}{DH}=\frac{AC}{AF}\)=> DH = AF. Tương tự: FH = AD
Do đó: Tứ giác AFHD là hình bình hành. Do AH cắt DF ở I => I là trung điểm AH và DF (T/c hbh)
Dễ thấy: Tứ giác BHCE là hình vuông, có HE giao BC ở G => G là trung điểm EH và BC
Xét \(\Delta\)AEH: I là trung điểm AH; G là trung điểm EH => IG là đường trung bình \(\Delta\)AEH => IG // AE (3)
\(\Delta\)CGF = \(\Delta\)BGK (c.g.c) => CF = BK => AF = BK (Do CF = AF)
Lại có: ^DBK = 3600 - ^ABD - ^ABC - ^GBK = 3600 - 450 - ^ABC - ^ACB - 450 = 900 + ^BAC
^DAF = ^BAC + ^BAD + ^CAF = ^BAC + 900
=> ^DAF = ^DBK. Xét \(\Delta\)ADF và \(\Delta\)BDK có: ^DAF = ^DBK; AD=BD; AF=BK => \(\Delta\)ADF = \(\Delta\)DBK (c.g.c)
=> ^ADF = ^BDK => ^ADF + ^BDF = ^BDK + ^BDF => ^ADB = ^FDK = 900
Xét \(\Delta\)DKF : I là trung điểm DF; G là trung điểm FK => IG là đường trung bình \(\Delta\)DKF => IG // DK
Mà DK vuông góc DF (Vì ^FDK = 900) nên IG vuông góc DF (4)
Từ (3) và (4) => AE vuông góc DF (Quan hệ song song vuông góc)
C/m tương tự, ta có: CD vuông góc EF; BF vuông góc DE
Từ đó: AE; BF; CD là 3 đường cao trong \(\Delta\)DEF => 3 đường AE; BF; CD đồng qui (đpcm).
Không vẽ hình vì sợ duyệt
Gọi I là giao điểm của BD và CF, ta cần chứng minh AE đi qua I.
\(\Delta ABF\)và \(\Delta ACD\)đều nên \(AB=AF,AD=AC\)và \(\widehat{BAF}=\widehat{DAC}=60^0\)
\(\Rightarrow\widehat{BAF}+\widehat{BAC}=\widehat{DAC}+\widehat{BAC}\)\(\Rightarrow\widehat{BAD}=\widehat{FAC}\)
Xét \(\Delta ABD\)và \(\Delta AFC\)ta có: \(AB=AF\left(cmt\right);\widehat{BAD}=\widehat{CAF}\left(cmt\right);AD=AC\left(cmt\right)\)
\(\Rightarrow\Delta ABD=\Delta AFC\left(c.g.c\right)\)\(\Rightarrow\hept{\begin{cases}\widehat{ABD}=\widehat{AFC}\\\widehat{ADB}=\widehat{ACF}\end{cases}}\)
Do B, I, D thẳng hàng và C, I ,F thẳng hàng nên ta có \(\hept{\begin{cases}\widehat{ABI}=\widehat{AFI}\\\widehat{ADI}=\widehat{ACI}\end{cases}}\)và từ đó ta có các tứ giác IAFB và IADC nội tiếp.
\(\Rightarrow\hept{\begin{cases}\widehat{AIB}+\widehat{AFB}=180^0\\\widehat{AIC}+\widehat{ADC}=180^0\end{cases}}\Rightarrow\hept{\begin{cases}\widehat{AIB}=180^0-\widehat{AFB}\\\widehat{AIC}=180^0-\widehat{ADC}\end{cases}}\)
Do các tam giác ABF và ACD đều nên \(\widehat{AFB}=\widehat{ADC}=60^0\), từ đó dễ dàng tính được \(\widehat{AIB}=\widehat{AIC}=120^0\)
Mà \(\widehat{AIB}+\widehat{AIC}+\widehat{BIC}=360^0\)nên ta cũng dễ dàng tính ra \(\widehat{BIC}=120^0\)
Mặt khác tam giác BCE đều nên \(\widehat{BEC}=60^0\)
Tứ giác IBEC có \(\widehat{BIC}+\widehat{BEC}=60^0+120^0=180^0\)nên tứ giác IBEC nội tiếp
\(\Rightarrow\widehat{BIE}=\widehat{BCE}\), lại có \(\widehat{BCE}=60^0\)do tam giác BCE đều nên \(\widehat{BIE}=60^0\)
Ta có \(\widehat{AIE}=\widehat{AIB}+\widehat{BIE}=120^0+60^0=180^0\)nên I thuộc AE hay AE đi qua I
Mà I chính là giao điểm của BD, CF
\(\Rightarrow\)AE, BD, CF đồng quy.