Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) M là trung điểm của BC
=> BM=CM
tam giác ABC cân tại A
=> AB=AC
xét tam giác ABM và tam giác ACM có
AB=AC
BM=CM
cạnh AM chung
do đó : tam giác ABM= tam giác ACM ( c.c.c)
b) do tam giác ABM = tam giác ACM
=> góc A1 = góc A2
xét tam giác AEM và tam giác AFM có
cạnh AM chung
góc A1= góc A2
góc AEM=góc AFM =90 độ
do đó tam giác AEM = tam giác AFM ( cạnh huyền - góc nhọn)
c) gọi N là giao của AM va EF
do tam giác AEM= tam giác AFM
=> AE=AF
xét tam giác AEN và tam giác AFN có
cạnh AN chung
góc A1 = góc A2
AE=AF
do đó tam giác AEN=tam giác AFN ( c.g.c)
=> góc N1=góc N2
mà góc N1 + góc N2 = 180 độ ( kề bù)
=> góc N1= góc N2=90 độ
=> AN vuông góc EF
hay AM vuông góc EF

mình không biết chỗ nào vẽ được hình cả , mong bạn thông cảm nha , bạn hỏi thầy cô giao ý

Hình tự vẽ
a, \(\Delta BAM\)và \(\Delta BDM\)có
\(\widehat{ABM}=\widehat{DBM}\left(gt\right)\)
\(AM\): cạnh chung
\(\widehat{BAM}=\widehat{BDM}\left(=90^o\right)\)
\(\Rightarrow\Delta BAM=\Delta BDM\left(ch-gn\right)\)
\(\Rightarrow BA=BD\)(2 cạnh tương ứng )
Để nghĩ tiếp :(
Ta có:
∠AMB+∠ABM=90o
∠BMD+∠MBD=900
Mà ∠AMB=∠BMD (gt)
=> ∠ABM=∠MBD
Xét ΔBAM và ΔBAM có:
∠ABM=∠MBD (gt)
BM chung
∠ABM=∠MBD (cmt)
=> ΔBAM = ΔBAM (g-c-g)
=> BA=BD (2 cạnh tương ứng)
b,Xét ΔABC và ΔDBE có:
∠ABC chung
∠BAC=∠BDM=90o
BA=BD (cmt)
=> ΔABC = ΔDBE (g-c-g)
c,Ta có
BC⊥ED
AK⊥ED
=> BC//AK hay BC//AN
=> ∠ANM=∠MBC ( 2 góc slt) (1)
Mà:
DH⊥AC
BA⊥AC
=> BA//DH hay BA//DN
=> ∠MND=∠ABM ( 2 góc so le trong) (2)
Mà ∠ABM=∠MBD ( vì BM là tia phân giác của góc ABC)
Từ(1) và (2) =>∠ANM=∠MND
=> NM là tia phân giác của góc HMK
d,Ta có BM là tia phân giác của góc ABC (3)
Và NM là tia phân giác của góc HMK
Vì ∠ANM=∠MBC
∠MND=∠ABM
=> ∠ANM=∠MBC=∠MND=∠ABM
=> BN là tia phân giác của góc ABC (4)
Từ (3) và (4) => B,M,N thẳng hàng

1.

Xét tam giác vuông AHE có FI là đường trung tuyến ứng với cạnh huyền nên IF = IH = IA = AH/2 = 6 : 2 = 3 (cm)
Do IF = IH nên tam giác IHF cân tại I. Vậy thì \(\widehat{IFH}=\widehat{IHF}\)
Lại có \(\widehat{IHF}=\widehat{BHE}\) nên \(\widehat{IFH}=\widehat{BHE}\) (1)
Xét tam giác vuông BFC có FK là đường cao đồng thời là trung tuyến nên KF = KC = KB = BC : 2 = 4 (cm)
Ta cũng có KF = KB nên \(\widehat{HFK}=\widehat{HBK}\) (2)
Ta có \(\widehat{HBE}+\widehat{BHE}=90^o\) (3)
Từ (1), (2), (3) suy ra \(\widehat{IFH}+\widehat{HFK}=90^o\Rightarrow\widehat{IFK}=90^o\)
Xét tam giác vuông IFK, áp dụng định lý Pi-ta-go ta có:
IK2 = IF2 + FK2 = 32 + 42 = 25
\(\Rightarrow IK=5cm.\)
2.
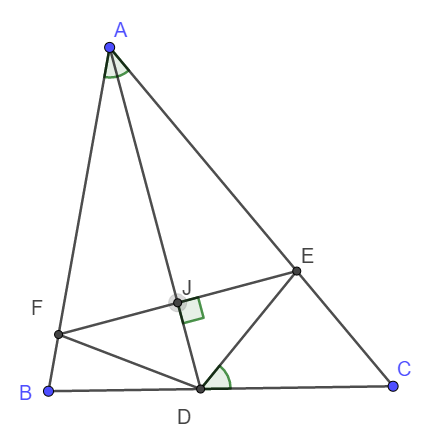
Gọi J là giao điểm của AD và EF.
Xét tam giác AFE có AJ là phân giác đồng thời đường cao nên AFE là tam giác cân tại A.
Vậy nên AJ đồng thời là trung trực của EF.
Lại có D thuộc AJ nên DE = DF. (1)
Xét tam giác AFD và tam giác AED có:
AF = AE
Cạnh AD chung
DF = DE
\(\Rightarrow\Delta AFD=\Delta AED\left(c-c-c\right)\)
\(\Rightarrow\widehat{AFD}=\widehat{AED}\Rightarrow\widehat{BFD}=\widehat{DEC}\)
Lại có \(\widehat{FBD}=180^o-\widehat{BAC}-\widehat{BCA}\)
\(\widehat{DEC}=180^o-\widehat{EDC}-\widehat{CBA}=180^o-\widehat{BAC}-\widehat{BCA}\)
Vậy nên \(\widehat{DBF}=\widehat{DFB}\) hay tam giác DBF cân tại D.
Suy ra DF = DB. (2)
Từ (1) và (2) suy ra DB = DF = DE.

Cho tam giác ABC cân tại A , có M là chung điểm của BC
a) CM :Tam Giác ABM = Tam giác ACM
b)Từ M kẻ ME vuông góc AB ;MF vuông góc AC (E thuộc AB ,F thuộc AC) .CM Tam giác AEM =Tam giác AFM
c)CM AM vuông góc EF
d) Trên tia MF lấy điểm I sao cho IM =FM . CM EI // AM
Giúp minh với ! minh h cho

Lấy X, Y lần lượt đối xứng A qua H và M.
Dễ thấy ΔΔAMB cân( đường cao đồng thời là phân giác)
suy ra ABXM là hình thoi
ta có M vừa là trung điểm BC vừa là trung điểm AY
=> ABYC là hình bình hành
suy ra CY=AB=XM và XMBˆ=ABCˆXMB^=ABC^ = MCYˆMCY^
=> CY∖∖XMCY∖∖XM
=>XYCM là hình bình hành=> MC=XY
mà ta còn có AC=BY ( hbh)
BX=AM ( hình thoi)
=> ΔAMC=ΔBXYΔAMC=ΔBXY
=> XBYˆ=MACˆ=XAYˆXBY^=MAC^=XAY^
mà AY∖∖BXAY∖∖BX
=>AXBY là hình thang cân
=>AB=XY=MC=MB=AM
=> tam giác AMB đều
=>BAMˆ=Bˆ=60oBAM^=B^=60o=>Aˆ=90o,C=30oˆ