Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
H1;H2 lần lượt là trực tâm tam giác OAB, OCD và \(\widehat{AOB}=\widehat{COD}\)(đối đỉnh)
=> \(\frac{OH_1}{OH_2}=\frac{AB}{CD}\)
Gọi M,N,K lần lượt là trung điểm của các đoạn thẳng AD, BC, BD
Vì G1;G2 lần lượt là trọng tâm của các tam giác OAD; OBC. Nên \(\frac{OG_1}{OM}=\frac{2}{3};\frac{OG_2}{ON}=\frac{2}{3}\)
\(\Delta\)OMN có: \(\frac{OG_1}{OM}=\frac{OG_2}{ON}\left(=\frac{2}{3}\right)\)=> G1G2 // MN và \(G_1G_2=\frac{2}{3}MN\)
\(OH_1\perp MK,OH_2\perp NK,MK=\frac{AB}{2},NK=\frac{CD}{2}\)
Do đó: \(\widehat{H_1OH_2}=\widehat{MKN},\frac{OH_1}{MK}=\frac{OH_2}{NK}\). Nên \(\Delta\)OH1H2 đồng dạng với \(\Delta\)KMN (cgc)
=> \(H_1H_2\perp MN\)Mà G1G2 // MN
Nên \(H_1H_2\perp G_1G_2\)=> \(S=\frac{1}{2}H_1H_2\cdot G_1G_2\)
Áp dụng BĐT Cosi cho 2 số dương ta có:
\(S=\frac{1}{2}H_1H_2\cdot G_1G_2=\frac{3G_1G_2\cdot H_1H_2}{6}\le\frac{\left(3G_1G_2+H_1H_2\right)^2}{24}\)
Dấu "=" <=> \(3G_1G_2=H_1H_2\Leftrightarrow OH_1=AB\)và \(OH_2=CD\)
\(\Leftrightarrow\widehat{AOB}=\widehat{COD}=45^o\)
Bài 2: *có nhiều cách làm bài này, mỗi cách có 1 hình khác nhau, đang lỗi nên không vẽ được hình*
Cách 1: Ta có: \(\widehat{BAC}=90^o\)(Góc nội tiếp chắn nửa đường tròn)
Đặt BH=x, ta có HC=HB-BH=2R-x
\(\Delta\)ABC vuông tại A, AH là đường cao
=> AH2=BH.HC. Nên \(AH=\sqrt{x\left(2R-x\right)}\)
Áp dụng BĐT Cosi cho 2 số dương, ta có: AH+BH=\(\sqrt{x\left(2R-x\right)+x}=\frac{1}{\sqrt{3+2\sqrt{2}}}\sqrt{x\left[\left(3+2\sqrt{2}\right)\left(2R-x\right)\right]}+x\)
\(\le\frac{1}{\sqrt{\left(\sqrt{2}+1\right)^2}}\cdot\frac{a+\left(3+2\sqrt{2}\right)\left(2R-x\right)}{2}+x\)\(=\frac{1}{\sqrt{2}+1}\left[\frac{x}{2}\left(\sqrt{2}+1\right)^2\cdot R-\frac{\left(\sqrt{2}+1\right)^2\cdot x}{2}\right]+x\)
\(=\frac{\sqrt{2}-1}{2}\cdot x+\left(\sqrt{2}+1\right)R-\frac{\sqrt{2}+1}{2}x+x=\left(\sqrt{2}+1\right)R\)
Ta có AB+AH \(\le\left(\sqrt{2}+1\right)R\)không đổi
Dấu "=" xảy ra <=> \(x=\left(3+2\sqrt{2}\right)\left(2R-x\right)\)
\(\Leftrightarrow x=\frac{2+\sqrt{2}}{2}R\)
\(\Leftrightarrow\widehat{AOC}=45^o\)
Cách 2: Gọi M là điểm trên nửa đường tròn (O) sao cho \(\widehat{COM}=45^o\) và gọi N là giao của nửa đường tròn (O) tại M với BC
Ta có: M,N cố định; \(\widehat{ONM}=45^o\), BN không đổi
Điểm A trên đường tròn (O)
Do đó tia NA nằm giữa 2 tia NB và NM
\(\Rightarrow\widehat{ANH}\le\widehat{ONM}=45^o\). Mà \(\widehat{ANH}+\widehat{HAN}=90^o\), Nên \(\widehat{HAN}\ge45^o\)
=> \(\widehat{ANH}\le\widehat{HAN},\)\(\Delta\)AHN có: \(\widehat{ANH}\le\widehat{HAN}\Rightarrow AH\le HN\)
Do đó: AH+BH \(\le\)HN+BH=BN, không đổi
Dấu "=" xảy ra <=> A = M
Vậy khi A trên nửa đường tròn (O) sao cho \(\widehat{COA}=45^o\) thì AH+BH lớn nhất

1/ Tinh ∆. Pt co 2 nghiem x1,x2 <=> ∆>=0.
Theo dinh ly Viet: S=x1+x2=-b/a=m+3.
Theo gt: |x1|=|x2| <=> ...
2/ \(\frac{\sin^2x-\cos^2x}{1+2\sin x.\cos x}\)
\(=\frac{\cos^2x\left(\frac{\sin^2x}{\cos^2x}-\frac{\cos^2x}{\cos^2x}\right)}{\cos^2x\left(\frac{1}{\cos^2x}+\frac{2\sin x.\cos x}{\cos^2x}\right)}\)
\(=\frac{\tan^2x-1}{\tan^2x+1+2\tan x}\)
\(=\frac{\left(\tan x-1\right)\left(\tan x+1\right)}{\left(\tan x+1\right)^2}\)
\(=\frac{\tan x-1}{\tan x+1}\left(dpcm\right)\)
c/ A M C B N BC=8 AC=7 AB=6
- Ta có: \(\overrightarrow{BA}^2=\left(\overrightarrow{CA}-\overrightarrow{CB}\right)^2\)
\(\Leftrightarrow BA^2=CA^2-2\overrightarrow{CA}.\overrightarrow{CB}+CB^2\)
\(\Leftrightarrow\overrightarrow{CA}.\overrightarrow{CB}=\frac{CA^2+CB^2-BA^2}{2}=\frac{77}{2}\)
- \(\overrightarrow{MN}^2=\left(\overrightarrow{CN}-\overrightarrow{CM}\right)^2=\left(\frac{3}{2}\overrightarrow{CB}-\frac{5}{7}\overrightarrow{CA}\right)^2\)
\(\Leftrightarrow MN^2=\frac{9}{4}CB^2-\frac{15}{7}\overrightarrow{CA}.\overrightarrow{CB}+\frac{25}{49}CA^2\)
\(=\frac{9}{4}.64-\frac{15}{7}.\frac{77}{2}+\frac{25}{49}.49\)
\(=\frac{173}{2}\)
\(\Rightarrow MN=\sqrt{\frac{173}{2}}=\frac{\sqrt{346}}{2}\)

#)Giải :
Lấy điểm C tùy ý trên mặt phẳng chứa n điểm, ta có :
\(\overrightarrow{CB_1}+\overrightarrow{CB_2}+...+\overrightarrow{CB_n}=\overrightarrow{CA_1}+\overrightarrow{CA_2}+...+\overrightarrow{CA_n}\)
\(\Rightarrow\left(\overrightarrow{CB_1}-\overrightarrow{CA_1}\right)+\left(\overrightarrow{CB_2}-\overrightarrow{CA_2}\right)+...+\left(\overrightarrow{CB_n}-\overrightarrow{CA_n}\right)=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{A_1B_1}+\overrightarrow{A_2B_2}+...+\overrightarrow{A_nB_n}=\overrightarrow{0}\left(đpcm\right)\)
²⁴ʱŤ.Ƥεɳɠʉїɳş༉ ( Team TST 14 ) : cái đoạn thứ 3 bỏ ngoặc với \(\overrightarrow{0}\) đi nhé !
Thay vào chỗ \(\overrightarrow{0}\)là :
\(=\left(\overrightarrow{CB_1}+\overrightarrow{CB_2}+...+\overrightarrow{CB_n}\right)-\left(\overrightarrow{CA_1}+\overrightarrow{CA_2}+...+\overrightarrow{CA_n}\right)\)
Vì n điểm \(B_1,B_2,....,B_n\)cũng là n điểm \(A_1,A_2,...,A_n\)nhưng được kí hiệu 1 cách khác nên ta có:
\(\overrightarrow{CB_1}+\overrightarrow{CB_2}+...+\overrightarrow{CB_n}=\overrightarrow{CA_1}+\overrightarrow{CA_2}+...+\overrightarrow{CA_n}\)
=> đpcm
ý kiến riêng của tớ =))
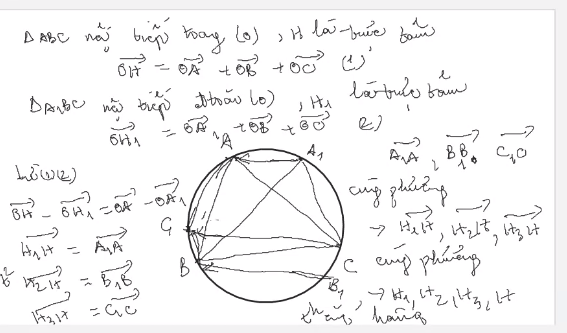
Nếu tam giác ABC và A1B1C1 có cùng trọng tâm G thì \(\overrightarrow{AA_1}+\overrightarrow{BB_1}+\overrightarrow{CC_1}=\overrightarrow{0}\) bạn biết cái này chưa ?
Rồi bạn