Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )

Xét ΔDCM và ΔABM có:
AM = MD ( GT )
BM = BC (AM là đường trung tuyến của ΔABC tại đỉnh A)
góc BMA = góc DMC ( hai góc đối đỉnh)
=> ΔDMC = Δ ABM (c.g.c)
=> Góc BAM = Góc MDC ( hai góc tương ứng)
mà Góc BAM và Góc MDC nằm ở vị trí so le trong
=> AB\\CD
b) xét ΔAKM và Δ DFM có
góc KMA = góc DMF ( 2 góc đối đỉnh)
góc BAM = góc MDC (cmt)
AM = MD ( GT )
=> ΔAKM = ΔDFM (g.c.g)
=> MK = MF ( 2 cạnh tương ứng)
=> M là trung điểm của KF
Học tốt

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\hat{AMB}=\hat{DMC}\) (hai góc đối đỉnh)
MB=MC
Do đó: ΔAMB=ΔDMC
=>AB=DC
ΔMAB=ΔMDC
=>\(\hat{MAB}=\hat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DC
b: Xét ΔMBA và ΔMCD có
\(\hat{MBA}=\hat{MCD}\) (hai góc so le trong, AB//CD)
MB=MC
\(\hat{BMA}=\hat{CMD}\) (hai góc đối đỉnh)
Do đó: ΔMBA=ΔMCD
=>MA=MD
=>M là trung điểm của AD
Giải:
Câu a:
Xét tứ giác ABCD có:
AM = MD (gt)
MB = MC (gt)
⇒ Tứ giác ABCD là hình bình hành(tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường thì tứ giác đó là hình bình hành)
Tứ giác ABCD là hình bình hành(cmt)
⇒ AB song song và bằng CD (đpcm)


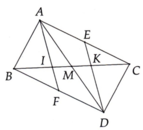
a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )