K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

TN
20 tháng 3 2020
Tự vẽ hình.
a) Xét tam giác OAB có AB // CD
⇒AOOC=OBOD=ABDC⇒12OC=93=18DC⇒AOOC=OBOD=ABDC⇒12OC=93=18DC ( Hệ quả định lý Ta - lét ) (1)
=> OC = 4cm, DC = 6cm
Vậy OC = 4cm và DC = 6cm
b) Xét tam giác FAB có DC // AB
⇒FDAD=FCCB⇒FD.BC=FC.AD⇒FDAD=FCCB⇒FD.BC=FC.AD ( ĐPCM )
c) Theo (1), ta đã có:
OAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBDOAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBD (2)
Vì MN // AB mà AB // DC => MN // DC
Xét tam giác ADC có MO// DC
⇒MODC=AOAC⇒MODC=AOAC ( Hệ quả định lý Ta - lét ) (3)
CMTT : ONDC=OBDBONDC=OBDB (4)
Từ (2), (3) và (4) => MODC=NODC⇒MO=NOMODC=NODC⇒MO=NO ( ĐPCM )
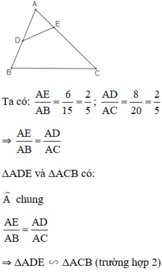
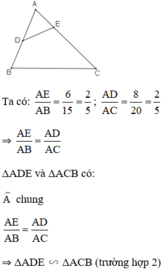
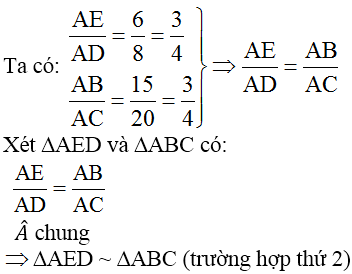
Sửa đề: Tam giác ABC vuông tại A. Câu c. C/m IB.AD=IC.AE
a.
Ta có:
\(\dfrac{AE}{AB}=\dfrac{6}{15}=\dfrac{2}{5};\dfrac{AD}{AC}=\dfrac{8}{20}=\dfrac{2}{5}\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Xét tam giác ABC và tam giác AED,có:
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\) ( cmt )
\(\widehat{A}:chung\)
Vậy tam giác ABC dồng dạng tam giác AED ( c.g.c )
b.
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{15^2+20^2}=\sqrt{625}=25cm\)
Ta có: tam giác ABC dồng dạng tam giác AED ( c.g.c )
\(\Rightarrow\dfrac{AD}{AC}=\dfrac{DE}{BC}\)
\(\Leftrightarrow\dfrac{2}{5}=\dfrac{DE}{25}\)
\(\Leftrightarrow5DE=50\)
\(\Leftrightarrow DE=10cm\)
c.Áp dụng t/c đường phân giác góc A, ta có:
\(\dfrac{AB}{AC}=\dfrac{IB}{IC}\)
Mà \(\dfrac{AB}{AC}=\dfrac{AE}{AD}\) ( 2 tam giác đồng dạng )
\(\Rightarrow\dfrac{AE}{AD}=\dfrac{IB}{IC}\)
\(\Leftrightarrow IB.AD=IC.AE\)
bạn kiểm tra lại đề nhé