Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của Tuấn Anh Nguyễn - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo link bài làm tương tự nhé!

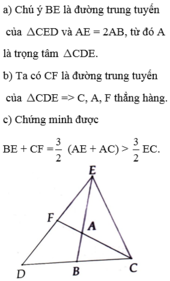
Cho tam giác ABC vuông tại A, BD là tia phân giác của góc B ( d thuộc AC). Kẻ DEvuông gócBC ( E thuộc BC). Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh rằng:
a) BD là đường trung trực của AF
b) AD < BC
c) Ba điểm E, D, F thẳng hàng

A B C F E M D
a)Xét ΔAME và ΔDMB có:
AM=DM(gt)
\(\widehat{AME}=\widehat{DMB}\left(đđ\right)\)
ME=MB(gt)
=> ΔAME=ΔDMB(c.g.c)
=> \(\widehat{AEM}=\widehat{DBM}\). Mà hai góc này ở vị trí sole trong
=> AE//BC
b)Xét ΔAMF và ΔDMC có:
AM=DM(gt)
\(\widehat{AMF}=\widehat{DMC}\left(đđ\right)\)
MF=MC(gt)
=> ΔAMF=ΔDMC(c.g.c)
=> \(\widehat{AFM}=\widehat{DCM}\). Mà hai góc này ở vị trí sole trong
=> AF//DC
Vì: AE//BC(cmt) ; AF//BC(cmt)
=> Ba điểm E,A ,F thẳng hàng
c) Xét ΔMBF và ΔMEC có:
MB=ME(gt)
\(\widehat{BMF}=\widehat{EMC}\left(đđ\right)\)
MF=MC(gt)
=>ΔMBF=ΔMEC(c.g.c)
=>\(\widehat{MFB}=\widehat{MCE}\). Mà hai góc này ở vị trí sole trong
=>BF//CE

Tham khảo
Câu hỏi của Hot girl 2k5 - Toán lớp 7 - Học toán với OnlineMath
mik ko hieu cau c cho lam, ai giang giup mik cau c voi :((

a) . Xét\(\Delta ABE\) và \(\Delta ADE\) có:
BA = DA (gt)
Góc BAE = góc DAE ( gt)
AE cạnh chung
nên \(\Delta ADE\) = \(\Delta ABE\)( c-g-c)
b) Ta có :\(\widehat{ABI}+\widehat{AIB}+\widehat{BAI}\)= \(^{180^o}\)
Suy ra : \(\widehat{AIB}\) = \(180^o\)- \(\widehat{ABI}-\widehat{BAI}\)
\(\widehat{AID}+\widehat{DAI}+\widehat{IDA}\)=\(^{180^o}\)
Suy ra: \(\widehat{AID}\) = \(180^O\) - \(\widehat{ADI}\)-\(\widehat{IAD}\)
Mà \(\widehat{BAI}=\widehat{IAD}\left(gt\right)\)
\(\widehat{ABI}=\widehat{ADI}\)(\(\Delta ABD\)cân tại A)
\(\Rightarrow\)\(\widehat{AID}=\widehat{AIB}\)
Ta có: \(\widehat{AID}+\widehat{AIB}=180^o\)( 2 GÓC KỀ BÙ )
MÀ \(\widehat{AID}=\widehat{AIB}\)( CHỨNG MINH TRÊN )
NÊN \(\widehat{AIB}=\widehat{AIB}=\frac{180^O}{2}=90^O\)
HAY \(AE\perp BD\)