Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

P/S 3 chữ hoa liên tiếp là góc :D
a,Ta có :\(AD//BC=>DAC=BCA\)
Xét Tam giác ABC và tam giác CDA
\(BC=DA\)(gt)
\(BCA=DAC\)(cmt)
\(CA\)cạnh chung
\(=>\Delta ABC=\Delta CDA\left(c-g-c\right)\)
b,Ta có : \(AD//BC=>ADB=CBD\)
Xét tam giác ABD và tam giác CDB
\(BC=AD\)(gt)
\(ADB=CBD\)(cmt)
\(BD\)cạnh chung
\(=>\Delta ABD=\Delta CDB\left(c-g-c\right)\)
c,Xét tam giác ODA và tam giác OBC
\(DBC=BDA\)(cm câu b)
\(AD=BC\)(gt)
\(DAC=ACB\)(cm câu a)
\(=>\Delta ODA=\Delta OBC\left(g-c-g\right)\)

b: Xét tứ giác ABCD có
AD//BC
AD=BC
Do đó: ABCD là hình bình hành
Suy ra: BA//CD

a, Xét \(\Delta ADC\) và \(\Delta ABC\) có:
\(AD=BC\left(gt\right)\)
\(\widehat{A1}=\widehat{C1}\) (So le trong ; \(AD//BC\) )
\(AC\) là cạnh chung
\(\Rightarrow\Delta ADC=\Delta ABC\left(c-g-c\right)\)
b,Ta có: \(\Delta ADC=\Delta ABC\left(cmt\right)\)
\(\Rightarrow\widehat{C2}=\widehat{A2}\) (2 góc tương ứng) và \(CD=AB\) (2 cạnh tương ứng)
\(\Rightarrow AB//CD\left(đpcm\right)\)
Xét \(\Delta ABD\) và \(\Delta CBD\) có:
\(CD=AB\left(cmt\right)\)
\(AD=CB\left(cmt\right)\)
\(BD\) là cạnh chung
\(\Rightarrow\Delta ABD=\Delta CBD\left(c-c-c\right)\left(đpcm\right)\)

D C A H B
a) Xét \(\Delta ABH\)có:
\(\widehat{BAH}+\widehat{ABH}+\widehat{AHB}=180^o\)( đl tổng 3 góc của 1 tam giác)
hay \(\widehat{BAH}+60^o+90^o=180^o\)
\(\Rightarrow\widehat{BAH}=30^o\)
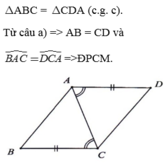
b) Xét \(\Delta ABC\)và \(\Delta CDA\)có:
\(AB=CD\left(gt\right)\)
\(\widehat{BAC}=\widehat{ACD}\)( 2 góc slt)
\(AC\)cạnh chung
\(\Rightarrow\Delta ABC=\Delta CDA\left(c-g-c\right)\)
\(\Rightarrow\widehat{ACB}=\widehat{CAD}\)( 2 góc tương ứng)
c) Ta có: \(\widehat{ACB}=\widehat{CAD}\)( c/mt)
Mà 2 góc này nằm ở vị trí slt
\(\Rightarrow AD//BC\)
\(\Rightarrow\widehat{AHB}=\widehat{HAD}\)(2 góc slt)
Mà \(\widehat{AHB}=90^o\left(gt\right)\)
\(\Rightarrow\widehat{HAD}=90^o\)
Hay nói cách AD vuông góc AH( đpcm)
học tốt!!

a) Vì \(AH\perp BC\Rightarrow\widehat{AHB}=90^o\)\(\Rightarrow\widehat{BAH}=90^o-\widehat{ABC}=90^o-60^o=30^o\)
b) Do \(AB//CD\Rightarrow\widehat{BAC}=\widehat{ACD}\)(2 góc so le trong)
\(\Rightarrow\Delta ABC=\Delta CDA\left(cgc\right)\)vì\(\hept{\begin{cases}AB=CD\\\widehat{BAC}=\widehat{ACD}\\ACchung\end{cases}}\)
c) Vì \(\Delta ABC=\Delta CDA\Rightarrow\widehat{ACB}=\widehat{CAD}\)(2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong của 2 đường thẳng AD và BC\(\Rightarrow AD//BC\)
Ta có \(AD//BC,AH\perp BC\Rightarrow AD\perp AH\)

xét tam giác ABC và tam giác CDA có AB=CD;BC=AD;AD chung
=>tam giác ABC=tam giác CDA
=>góc ACB=góc DAC(2 góc tương ứng)
mà 2 góc này có vị trí so le trong nên AB//CD
mà AH vuông góc BC nên AH vuông góc CD