Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

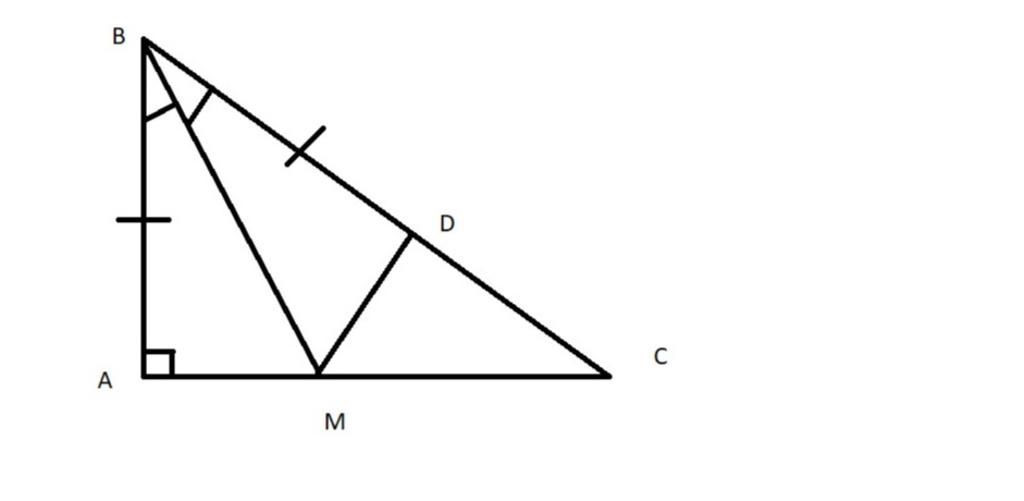

a)Xét △ABM và △△ DBM , ta có :
AB=BD(gt)
ˆABM^ == ˆDBM^ ( vì BM là tia phân giác của ˆABC^ )
BM là chung
⇒ △△ ABM= △△ DBM(c−g−c)
b)Ta có : ˆBAM^ == ˆBDM (( vì △ ABM= △ DBM)
Mà ˆBAM^ =90o(=90) ( vì △ ABC vuông tại A)
⇒⇒ ˆBDM=90o
⇒MD⇒ ⊥⊥ BC
c) Vì MD⊥⊥ BC(cmt)
⇒ ˆMDC^ =90o=90
⇒ △ MDC vuông tại D
⇒MC>MD(ch>cgv)
Mà MD=MA( vì △ABM=△ DBM)
⇒MC>MA

bạn ơi chứng minh tam giác ABM=tam giác ACM rồi sao lại còn chứng minh tiếp

Do MA và MC không đổi =>Để AM^2+BM^2+CM^2 nhỏ nhất =>AM là đường cao của tam giác ABC (1)
Mà ABC vuông cân =>M là trung điểm của BC
Kẻ MI vuông góc với AB,MK vuông góc với AC
suy ra MI // Ak,AI // MK suy ra AIMK là hình chữ nhật
Ta có :AM^2+BM^2+CM^
=AI^2+IM^2+IM^2+IB^2+CK^2+MK^2
=2AI^2+2IM^2+AM^2
=2*(AI^2+IM^2)+AM^2
=3AM^2
Từ (1) => AM^2+BM^2+c

1.
Xét tam giác AMB và tam giác NMC có:
AM = NM (gt)
AMB = NMC (2 góc đối đỉnh)
MB = MC (M là trung điểm của BC)
=> Tam giác AMB = Tam giác NMC (c.g.c)
Xét tam giác AMC và tam giác NMB có:
AM = NM (gt)
AMC = NMB (2 góc đối đỉnh)
MC = MB (M là trung điểm của BC)
=> Tam giác AMC = Tam giác NMB (c.g.c)
2.
Xét tam giác AME và tam giác BMC có:
AM = BM (M là trung điểm của AB)
AME = BMC (2 góc đối đỉnh)
ME = MC (gt)
=> Tam giác AME = Tam giác BMC (c.g.c)
=> AEM = BCM (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AE // BC
Xét tam giác ANF và tam giác CNB có:
AN = CN (N là trung điểm của AC)
ANF = CNB (2 góc đối đỉnh)
NF = NB (gt)
=> Tam giác ANF = Tam giác CNB (c.g.c)
=> AF = CB (2 cạnh tương ứng)

a: Xét ΔAME và ΔDMB có
MA=MD
\(\widehat{AME}=\widehat{DMB}\)
ME=MB
Do đó: ΔAME=ΔDMB
Xét tứ giác AEDB có
M là trung điểm của AD
M là trug điểm của EB
Do đó: AEDB là hình bình hành
Suy ra: AE//BC
b: Xét tứ giác AFDC có
M là trug điểm của AD
M là trung điểm của FC
Do đó: AFDC là hình bình hành
Suy ra: AF//BC
mà AE//BC
và AF,AE có điểm chug là A
nên E,A,F thẳng hàng

b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: CD//AB
