Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:Áp dụng định lý Menelaus với tam giác $AMC$ có $B,I,D$ thẳng hàng:
$\frac{AD}{DC}.\frac{IM}{IA}.\frac{BC}{BM}=1$
$\Leftrightarrow \frac{AD}{DC}.2.3=1$
$\Leftrightarrow \frac{AD}{DC}=\frac{1}{6}$
$\Rightarrow \frac{AD}{DC}=\frac{1}{7}$

a: góc BAE+góc CAE=90 độ
góc BEA+góc HAE=90 độ
mà góc CAE=góc HAE
nên góc BAE=góc BEA
=>ΔBAE cân tại B
c: góc CAD+góc BAD=90 độ
góc CDA+góc HAD=90 độ
mà góc BAD=góc HAD
nên góc CAD=góc CDA
=>ΔCAD cân tại C

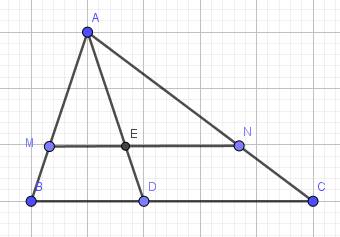
\(\Delta ABC\) có:
\(\dfrac{AM}{AB}=\dfrac{8}{12}=\dfrac{2}{3}\)
\(\dfrac{AN}{AC}=\dfrac{12}{15}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{2}{3}\)
\(\Rightarrow\) MN // BC (định lý Ta-lét)
\(\Delta AME\) và \(\Delta ABD\) có:
ME // BD (do MN // BC)
\(\Rightarrow\dfrac{AE}{AD}=\dfrac{AM}{AB}=\dfrac{2}{3}\) (hệ quả của định lý Ta-lét)

A B C M D F E
Kẻ MF // BC; F \(\in\)AC mà D \(\in\)AC nên F cũng \(\in\)DC
Xét \(\Delta\)DBC có : M là trung điểm của DB ( gt ); MF // BC ( F \(\in\)DC )
\(\Rightarrow\)F là trung điểm của DC ( Định lí 1 )
Lại xét \(\Delta\)DBC có : M là trung điểm của DB ( gt ); F là trung điểm của DC ( cmt )
\(\Rightarrow\)MF là đường trung bình của \(\Delta\)DBC ( Định nghĩa )
\(\Rightarrow MF=\frac{1}{2}BC\Rightarrow\frac{MF}{BC}=\frac{1}{2}\)( Định lý 2 ) (*)
Vì \(\frac{AD}{DC}=\frac{1}{2}\); F là trung điểm của DC hay \(\frac{FD}{DC}=\frac{FC}{DC}=\frac{1}{2}\) \(\Rightarrow\)AD = DF = FC \(\Rightarrow\frac{\text{AF}}{AC}=\frac{AD+\text{AF}}{AC}=\frac{2\cdot AD}{AC}=\frac{2\cdot1}{3}=\frac{2}{3}\)
Xét \(\Delta\)AEC ( MF // EC vì MF // BC mà E \(\in\)BC ) ta có :
\(\frac{\text{AF}}{AC}=\frac{MF}{EC}=\frac{2}{3}\)( Áp dụng định lý Ta-lét ) (**)
Ta lại có : \(\frac{MF}{BC}:\frac{MF}{EC}=\frac{MF\cdot EC}{BC\cdot MF}=\frac{EC}{BC}\)(***)
Từ (*)(**)(***) nên ta có : \(\frac{EC}{BC}=\frac{1}{2}:\frac{2}{3}=\frac{1\cdot3}{2\cdot2}=\frac{3}{4}\)\(\Rightarrow\frac{EB}{BC}=1-\frac{3}{4}=\frac{1}{4}\)
\(\Rightarrow\frac{EC}{EB}=\frac{3}{1}=3\)


mình không biết