Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

theo định lý thales ta có: \(\frac{CP}{NP}=\frac{CB}{AB}\) (1)
xét tứ giác BMNP có:
MN // BP và NP // MB
⇒ tứ giác BMNP là hình bình hành
⇒ MB = NP (2)
ta có: AB = MB + MA = \(\frac12MB+MB=\frac32MB\) (3)
(1) (2) (3) ta có: \(\frac{CP}{MB}=\frac{CB}{\frac32MB}\)
\(\Rightarrow CP=\frac23CB\Rightarrow CP\cdot\frac32=CB\)
\(\Rightarrow CB=\frac32\cdot6=9\left(\operatorname{cm}\right)\)
vậy CB = 9cm
BC bằng 9 cm. Các bước giải: Tìm tỉ lệ AM/AB: Vì 2.MA = MB, tỉ lệ AM so với toàn bộ AB là 1/3. Sử dụng định lý Thales: Vì MN song song với BC, tỉ lệ AN/AC cũng là 1/3. Tìm tỉ lệ CN/AC: Vì AN chiếm 1/3 AC, phần còn lại CN sẽ chiếm 2/3 AC. Sử dụng định lý Thales lần nữa: Vì NP song song với AB, tỉ lệ CP/CB cũng bằng tỉ lệ CN/AC, tức là 2/3. Tính BC: Theo đề bài, PC = 6 cm. Từ tỉ lệ CP/CB = 2/3, ta có 6/BC = 2/3, suy ra BC = 9 cm.

M nằm giữa A và B nên: AB = AM + MB = 10cm
Theo định lí Ta let ta có:
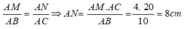
Chọn đáp án A

a: Xét ΔABC co AI là phân giác
nên IB/IC=AB/AC
=>AB/6=3/4,5=2/3
=>AB=4cm
Xét ΔBAC có MI//AC
nên MI/AC=BM/BA=BI/BC=3/7,5=2/5
=>MI/6=BM/4=2/5
=>MI=12/5cm; BM=8/5cm
b: MB/MA=BI/IC=BA/AC

Ta có: AB=AM+MB=8+11=19
Vì MN//BC (gt)
=>\(\frac{AM}{AB}=\frac{AN}{AC}\Rightarrow AN=\frac{AM.AC}{AB}=\frac{11.24}{19}=\frac{264}{19}\left(cm\right)\)
=>NC=24-AN bạn tự tính

ta có AM+BM=AB
AB=11+8=19
ta có MM//BC
\(\frac{AM}{AB}=\frac{AN}{AC}\)
mà \(\frac{AM}{AB}=\frac{11}{19}\)
\(\frac{AN}{24}=\frac{11}{19}\)
AN=\(\frac{24.11}{19}\)
Bài này bạn dùng đlý Ta -let là ra mà!