Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình giải theo cách lớp 5.
a) Có: \(AN+NC=AC\) mà \(AN=\dfrac{1}{2}NC\)
\(\Rightarrow\dfrac{1}{2}NC+NC=AC\Rightarrow\dfrac{3}{2}NC=AC\Rightarrow NC=\dfrac{2}{3}AC\)
\(2AN=\dfrac{2}{3}AC\Rightarrow AN=\dfrac{2}{3}.\dfrac{1}{2}AC=\dfrac{1}{3}AC\)
\(\dfrac{S_{ABN}}{S_{ABC}}=\dfrac{AN}{AC}=\dfrac{1}{3}\Rightarrow S_{ABN}=\dfrac{1}{3}S_{ABC}\left(1\right)\)
\(\dfrac{S_{ACM}}{S_{ABC}}=\dfrac{AM}{AB}=\dfrac{1}{3}\Rightarrow S_{ACM}=\dfrac{1}{3}S_{ABC}\left(2\right)\)
Từ (1) và (2) suy ra:
\(S_{ABN}=S_{ACM}\)
\(\Rightarrow S_{ABN}-S_{AMON}=S_{ACM}-S_{AMON}\)
\(\Rightarrow S_{MOB}=S_{NOC}\).
b) \(\dfrac{S_{AMC}}{S_{AMN}}=\dfrac{AC}{AN}=3\Rightarrow S_{AMC}=3S_{AMN}=3.4,5=13,5\left(cm^2\right)\)
\(\dfrac{S_{ABC}}{S_{AMN}}=\dfrac{AB}{AM}=3\Rightarrow S_{ABC}=3S_{AMN}=3.13,5=40,5\left(cm^2\right)\)
\(\dfrac{S_{NCB}}{S_{ABC}}=\dfrac{NC}{AC}=\dfrac{2}{3}\Rightarrow S_{NCB}=\dfrac{2}{3}S_{ABC}=\dfrac{2}{3}.40,5=27\left(cm^2\right)\)

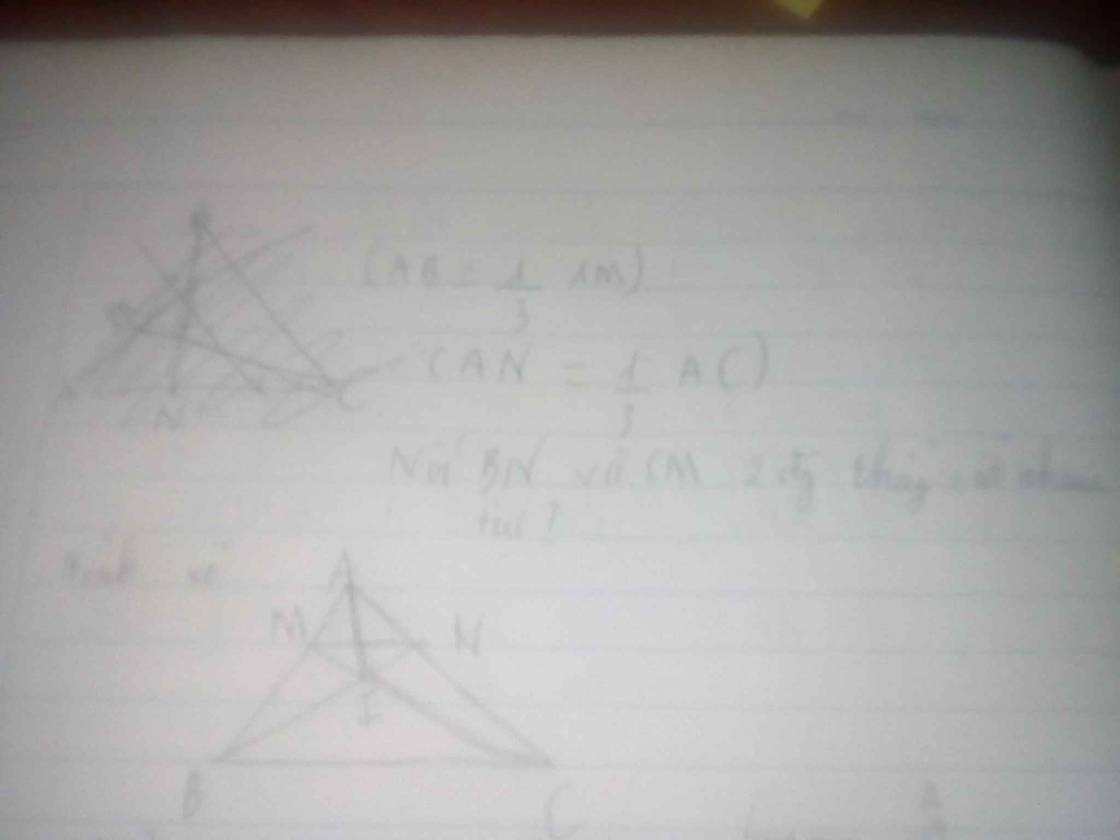 cái này là hình vẽ nhé!
cái này là hình vẽ nhé!
a, Tam giác AIB và tam giác ABC có chung chiều cao hạ từ B xuống AC, đáy AN = 1/3 đáy AC.
=> SAIB = 1/3 x S ABC.
Tam giác AIC và ABC có chiều cao hạ từ C xuống ABC, đáy AM = 1/3 đáy ABC.
=> SAIC = 1/3 x SABC.
=> SAIB = SAIC ( Vì cùng bằng = 1/3 SABC)
câu b thì bạn chưa nói rõ nên mình đưa bạn bản mẫu là tứ giác và 90cm2 nhé!
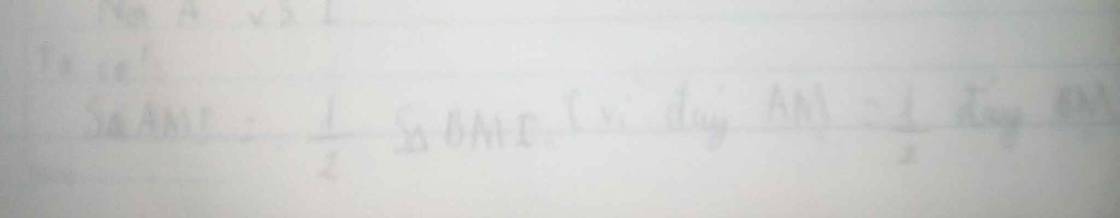 Ta có :
Ta có :
SAMI = 1/2 SƠMI ( vì đáy ÂM = 1/2 đáy BM)
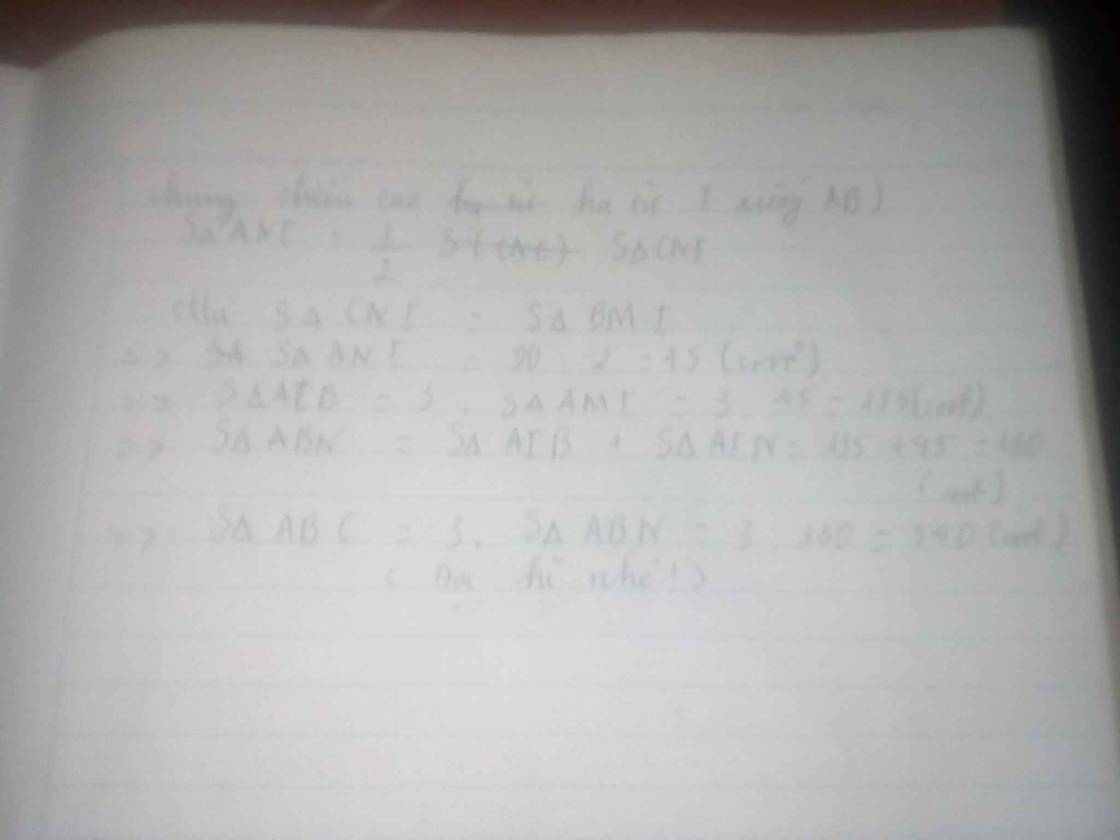 bạn thông cảm vì máy chụp hơi kém nhé!
bạn thông cảm vì máy chụp hơi kém nhé!

S(AKN) = 1/3S(NKC)
=>S(ABK) = 1/3S(BCK)
Mà S(AKM) = S(BKM) = 1/2 S(ABK) = 1/2 x 1/3=1/6S(BKC)
Mặt khác:
S(AKM) = S(BKM)
=> S(AKC) = SBKC)
=> S(BKC) = 42 :(1+1+6+6) x 6 =18 cm2

đề này đúng ra nó phải cho thêm dữ kiện về AB,AC chứ bạn

S(AKN) = 1/3S(NKC) =>S(ABK) = 1/3S(BCK) Mà S(AKM) = S(BKM) = 1/2 S(ABK) = 1/2 x 1/3=1/6S(BKC) Mặt khác: S(AKM) = S(BKM) => S(AKC) = SBKC) => S(BKC) = 42 :(1+1+6+6) x 6 =18 c m 2