
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


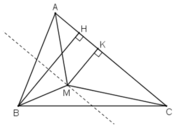
Kẻ đường cao BH, MK.
Ta có: SAMB + SBMC + SMAC = SABC (1)
Mà SAMB + SBMC = SMAC (2)
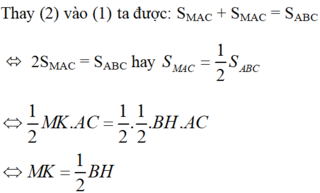
Do đó, M nằm trong ΔABC, nằm trên đường thẳng d bờ AC chứa B sao cho khoảng cách từ M đến AC = 1/2 đường cao BH.
Suy ra điểm M nằm trong ΔABC nằm trên đường trung bình của ΔABC.

SAMB+SBMC=SMAC đặt là S1+S2=S3 và SABC=S
Ta có S1+S2+S3=S=> S1+S2=S-S3 = S3
=> S3/S=1/2
S và S3 có chung cạnh đáy AC => chiều cao ứng với AC cua S3 = 1/2 chiều cao ứng với AC của S
Vậy ta dựng đg cao BH ( H thuộc AC), lấy trung điểm M của BH, qua M vẽ đg thẳng d//BC cắt AB và AC tại O và P
=> điểm M nằm trên OP thì S1+S2=S3

a) Xét tứ giác AETD có
TE//AD(gt)
TD//AE(gt)
Do đó: AETD là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Lời giải:
Lấy $K, H$ lần lượt đối xứng với $M$ qua $AB,AC$.
Theo tính chất đối xứng: $EK=EM; FM=FH$
Chu vi tam giác $MEF$:
$ME+EF+MF=EK+FH+EF\geq KH(*)$
Vì $M$ cố định và tam giác $ABC$ cố định nên $KH$ cố định
Vậy chu vi $MEF$ nhỏ nhất bằng $KH$. Điều này xảy ra khi $E,F$ là giao điểm của $KH$ với lần lượt $AB,AC$

A A A B B B C C C M M M D D D E E E
Do E đối xứng với M qua AC nên AC là đường trung trực EM.
Do đó AE = AM (1). Tương tự AD = AM (2)
Cộng theo vế (1) và (2) suy ra AE + AD = 2AM. (3)
*Chứng minh A, E, D thẳng hàng
Theo (1) thì AE = AM -> tam giác AEM cân tại A.
Do đó \(\widehat{EAM}=180^o-2\widehat{EMA}\)(4)
Tương tự \(\widehat{MAD}=180^o-2\widehat{AMD}\)(5)
Cộng theo vế (4) và (5) suy ra ^EAD = 180o do đó D, E, A thẳng hàng => AE + AD = ED
Kết hợp (3) ED = 2AM . Hạ \(AH\perp BC\) thì \(AM\ge AH\)
Đẳng thức xảy ra khi M trùng H.
Do đó \(ED\ge2AM\ge2AH=const\)
Đẳng thức xảy ra khi M trùng H hay M là chân đường cao hạ từ A đến BC.
P/s: Mới học dạng này nên ko chắc..

tam giác ABC vuông ở A cho ta góc BAC =90 độ
MD vuông góc với AB => góc MDA =90 độ
ME vuông góc với AC => góc MEA =90 độ
=> tứ giác ADME là hình chữ nhật => DE=AM =>DE min<=> AM min <=> AM vuông góc với BC
Vậy M là chân đường cao kẻ từ A , M thuộc BC thì DE có độ dài nhỏ nhất
