Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
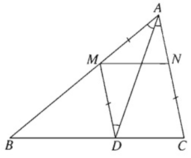
Giả sử đã dựng được hai điểm M, N thỏa mãn điều kiện đầu bài. Đường thẳng qua M và song song với AC cắt BC tại D. Khi đó tứ giác MNCD là hình bình hành. Do đó CN = DM. Từ đó suy ra tam giác AMD cân tại M. Do đó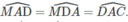 
. Suy ra AD là phân giác trong của góc A. Do đó AD dựng được .Ta lại có
N
M
→
=
C
D
→
, nên có thể xem M là ảnh của N qua phép tịnh tiến theo vectơ
D
C
→
.
Từ đó suy ra cách dựng:
- Dựng đường phân giác trong của góc A. Đường này cắt BC tại D.
- Dựng đường thẳng d là ảnh của đường thẳng AC qua phép tịnh tiến theo vectơ C D → . d cắt AB tại M.
- Dựng N sao cho N M → = C D → .
Khi đó dễ thấy M, N thỏa mãn điều kiện đầu bài.
\(BC\) \(\subset\)\(\left(SBC\right)\)
Tìm giao tuyến của của \(\left(OMN\right)\)và \(\left(SBC\right)\):
\(N\)là điểm chung thứ nhất
Ta có : \(MO\)\(\subset\)\(\left(AMO\right)\)\(\equiv\)\(\left(SAH\right)\)với \(H=AO\)\(\cap\) \(BC\)
\(\left(SAH\right)\)\(\cap\) \(\left(SBC\right)\)= \(SH\)
Trong \(\left(SAH\right)\): \(MO\)\(\cap\) \(SH\)= \(K\)
\(K\)là điểm chung thứ 2.
Vậy \(\left(OMN\right)\)\(\cap\)\(\left(SBC\right)\)= \(NK\)
Trong \(\left(SBC\right):\)\(NK\)\(\cap\)\(BC\)= \(P\)
Vậy \(\left(OMN\right)\)\(\cap\) \(BC\)= \(P\)
Ta có N thuộc (OMN)
C thuộc đường thẳng BC
Mà N trùng với C => N là giao điểm của (OMN) và BC
a: Trong mp(ABC), gọi E là giao điểm của MN và BC
\(O\in\left(OMN\right);O\in\left(BCD\right)\)
=>\(O\in\left(OMN\right)\cap\left(BCD\right)\)
\(E\in MN\subset\left(OMN\right);E\in BC\subset\left(BCD\right)\)
=>\(E\in\left(OMN\right)\cap\left(BCD\right)\)
Do đó: \(\left(OMN\right)\cap\left(BCD\right)=OE\)
b: Chọn mp(BCD) có chứa DB
\(\left(OMN\right)\cap\left(BCD\right)=OE\)
Gọi F là giao của OE với DB
=>F là giao của DB với mp(OMN)
Chọn mp(BCD) có chứa DC
\(\left(OMN\right)\cap\left(BCD\right)=OE\)
Gọi K là giao của OE với DC
=>K là giao của DC với mp(OMN)
2:
a: \(B\in SB\)
\(B\in\left(ABC\right)\)
Do đó: \(B=SB\cap\left(ABC\right)\)
b: Chọn mp(SAB) có chứa BH
\(SA\subset\left(SAB\right)\)
\(SA\subset\left(SAC\right)\)
Do đó: \(\left(SAB\right)\cap\left(SAC\right)=SA\)
Gọi E là giao của BH và SA
=>E là giao điểm cần tìm
c: Chọn mp(SBC) có chứa BK
\(SC\subset\left(SBC\right)\)
\(SC\subset\left(SAC\right)\)
Do đó: \(\left(SBC\right)\cap\left(SAC\right)=SC\)
Gọi F là giao của BK với SC
=>F là giao điểm cần tìm
d: Trong mp(SAC), gọi O là giao của HK với AC
mà \(AC\subset\left(ABC\right)\)
nên \(O=HK\cap\left(ABC\right)\)
1:
a: \(S\in SA\)
\(S\in SB\subset\left(SBC\right)\)
Do đó: \(S=SA\cap\left(SBC\right)\)
b: Chọn mp(SAB) có chứa SM
\(AB\subset\left(ABC\right)\)
\(AB\subset\left(SAB\right)\)
Do đó: \(AB=\left(SAB\right)\cap\left(ABC\right)\)
\(M\in AB\)
=>SM giao AB=M
=>\(M=SM\cap\left(ABC\right)\)
c: Chọn mp(BAC) có chứa MN
\(BC\subset\left(BAC\right)\)
\(BC\subset\left(SBC\right)\)
Do đó: (BAC) giao (SBC)=BC
mà \(BC\cap MN=N\)
nên \(N=MN\cap\left(SBC\right)\)
d: Chọn mp(ABC) có chứa MN
\(AC\subset\left(SAC\right)\)
\(AC\subset\left(ABC\right)\)
Do đó: \(AC=\left(SAC\right)\cap\left(ABC\right)\)
Gọi giao của MN và AC là E
=>\(E=MN\cap\left(SAC\right)\)
a) Nhận xét:
Do giả thiết cho IJ không song song với CD và chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K = IJ ∩ CD.
Ta có: M là điểm chung thứ nhất của (ACD) và (IJM);
Vậy (MIJ) ∩ (ACD) = MK
b) Với L = JN ∩ AB ta có:
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P = JL ∩ AD, Q = PM ∩ AC
Ta có:
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ = (ABC) ∩ (MNJ).
