
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



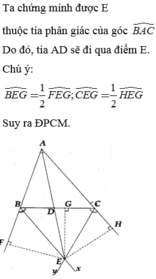
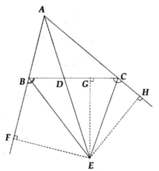
Gọi F,H,G lần lượt là hình chiếu vuông góc của điểm E xuống các đường thẳng AB, AC và BC.
Từ giả thiết suy ra EF = EG và EH = EG.
=> EF = EH nên E thuộc tia phân giác của góc BAC.
Mà AD là tia phân giác của góc BAC.
Vậy ba điểm A, D, E thẳng hàng.

Xét ΔABC có \(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{ABC}+\widehat{ACB}=180^0-30^0=150^0\)
=>\(2\cdot\left(\widehat{KBC}+\widehat{KCB}\right)=150^0\)
=>\(\widehat{KBC}+\widehat{KCB}=75^0\)
XétΔKBC có \(\widehat{KBC}+\widehat{KCB}+\widehat{BKC}=180^0\)
=>\(\widehat{BKC}=180^0-75^0=105^0\)
Vì BK và BH là hai tia phân giác của hai góc kề bù
nên BK\(\perp\)BH
=>\(\widehat{KBH}=90^0\)
Vì CK và CH là hai tia phân giác của hai góc kề bù
nên CK\(\perp\)CH
=>\(\widehat{KCH}=90^0\)
Xét tứ giác KBHC có \(\widehat{KBH}+\widehat{KCH}+\widehat{BKC}+\widehat{BHC}=360^0\)
=>\(\widehat{BHC}+105^0+90^0+90^0=360^0\)
=>\(\widehat{BHC}=75^0\)

a/ Ta có AB=AC(gt)
Mà D và E là trung điểm của AB và AC
=> AD=BD=AE=EC
Xét tam giác ABE và tam giác ACD có:
AB=AC(gt)
Góc A chung
AE=AD(cmt)
=> tam giác ABE= tam giác ACD(c-g-c)
b/ Ta có tam giác ABE= tam giác ACD(c-g-c)
=> góc ABE=góc ACD
=> góc KBC=góc KCB vì tam giác ABC cân tại A
Vậy tam giác KBC cân tại K