Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D
a sai vì nếu tam giác ABC thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC vuông tại A không phải vuông tại B.
b, c, d đúng.

a) Nếu ABC là một tam giác cân thì ABC là tam giác đều
Đây là mệnh đề sai
b) Nếu ABC là một tam giác cân và có một góc bằng 60o thì ABC là một tam giác đều
Đây là mệnh đề đúng

Lời giải:
Ta có: $S_{ABC}=\frac{h_a.a}{2}$
$S_{ABC}=\sqrt{p(p-a)(p-b)(p-c)}$ theo công thức Heron.
$\Rightarrow \frac{h_a.a}{2}=\sqrt{p(p-a)(p-b)(p-c)}$
$\Leftrightarrow \frac{a\sqrt{p(p-a)}}{2}=\sqrt{p(p-a)(p-b)(p-c)}$
$\Leftrightarrow \frac{a}{2}=\sqrt{(p-b)(p-c)}$
$\Rightarrow \frac{a}{2}=\frac{1}{2}\sqrt{(a+c-b)(a+b-c)}$
$\Rightarrow a^2=(a+c-b)(a+b-c)$$\Leftrightarrow a^2=a^2-(b-c)^2\Rightarrow (b-c)^2=0$
$\Rightarrow b=c$ hay $ABC$ là tam giác cân.

a)
\(P \Rightarrow Q\): “Nếu tam giác ABC là tam giác vuông tại A thì các cạnh của nó thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\)”
Mệnh đề này đúng.
\(Q \Rightarrow P\): “Nếu tam giác ABC có các cạnh thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\) thì tam giác ABC vuông tại A”
Mệnh đề này đúng.
\(P \Leftrightarrow Q\): “Tam giác ABC là tam giác vuông tại A khi và chỉ khi các cạnh của nó thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\)”
Mệnh đề này đúng do các mệnh đề \(P \Rightarrow Q,Q \Rightarrow P\)đều đúng.
\(\overline P \Rightarrow \overline Q \): “Nếu tam giác ABC không là tam giác vuông tại A thì các cạnh của nó thỏa mãn \(A{B^2} + A{C^2} \ne B{C^2}\)”
Mệnh đề này đúng.
b) Mệnh đề \(P \Rightarrow Q\) có thể phát biểu là:
“Tam giác ABC là tam giác vuông tại A là điều kiện đủ để tam giác ABC có các cạnh thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\)”
“Tam giác ABC có các cạnh thỏa mãn \(A{B^2} + A{C^2} = B{C^2}\) là điều kiện cần để tam giác ABC vuông tại A”
c)
X là tập hợp các tam giác ABC vuông tại A.
Y là tập hợp các tam giác ABC có trung tuyến \(AM = \frac{1}{2}BC\).
Dễ thấy: \(X \subset Y\) do các tam giác ABC vuông thì đều có trung tuyến \(AM = \frac{1}{2}BC\).
Ta chứng minh: Nếu tam giác ABC có trung tuyến \(AM = \frac{1}{2}BC\) thì tam giác ABC vuông tại A.
Thật vậy, \(BM = MC = AM = \frac{1}{2}BC\) suy ra M là tâm đường tròn đường kính BC, ngoại tiếp tam giác ABC.
\( \Rightarrow \widehat {BAC} = {90^ \circ }\) (góc nội tiếp chắn nửa đường tròn)
Vậy tam giác ABC là tam giác vuông.
Do đó \(Y \subset X\)
Vậy \(X = Y\)

Chọn D.
+ Phương án A: Do ![]()
Loại A.
+ Phương án B: ![]() và
và ![]() nên
nên ![]()
Loại B.
+ Phương án C: Do ![]() và
và ![]() không cùng phương.
không cùng phương.
Loại C.
+ Phương án D: AB = BC = CA 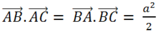

a) "Nếu ABC là một tam giác đều thì AB = BC = CA", cả hai mệnh đề đều đúng
b) "Nếu \(\widehat{C}>\widehat{A}\) thì AB > BC". Cả hai mệnh đề đều đúng
c) "Nếu ABC là một tam giác vuông thì \(\widehat{A}=90^0\)"
Nếu tam giác ABC vuông tại B (hoặc C) thì mệnh đề đảo sai

a.
Gọi (D):y=ax+b chứa điểm A, C
(D'):y=a'x+b' chứa điểm B, C
* Ta có: A thuộc (D) khi 1= 2a+b (1)
C thuộc (D) khi 4= 3a+b (2)
Giải hệ (1), (2) ta suy ra a=3 , b=-5
* Ta có: B thuộc (D') khi 3=6a'+b' (3)
C thuộc (D') khi 4=3a'+b' (4)
Giải hệ (3), (4) ta suy ra a=-1/3 , b= 5
Ta thấy: a.a' = 3.(-1/3)=-1
Suy ra (D) vuông góc (D') tại điểm chung C của của 2 cạnh (5)
Vậy tam giác ABC vuông tại C
Theo công thức tính cạnh của đoạn thẳng trong hệ trục tọa độ ta có:
AC=\(\sqrt{\left(x_A-x_C\right)^2+\left(y_A-y_C\right)^2}=\sqrt{\left(2-3\right)^2+\left(1-4\right)^2}\)\(=\sqrt{10}\)
BC=\(\sqrt{\left(x_B-x_C\right)^2+\left(y_B-y_C\right)^2}=\sqrt{\left(6-3\right)^2+\left(3-4\right)^2}\)\(=\sqrt{10}\)
Vậy AC=BC (6)
Từ (5) và (6) ta suy ra tam giác ABC vuông cân tại C
SABC=\(\dfrac{1}{2}\).AB.BC=\(\dfrac{1}{2}.\sqrt{10}.\sqrt{10}=\dfrac{1}{2}.10=\)5 (đvdt)
b. Làm tương tự câu a tìm độ dài các cạnh AB, BD, DA và tính diện tích bằng công thức SABD=\(\sqrt{p\left(p-AB\right)\left(p-BD\right)\left(p-DA\right)}\) với p là nửa chu vi tam giác ABD \(p=\dfrac{1}{2}\left(AB+BD+DA\right)\)
Tiếp tục dùng công thức SABD=\(=\dfrac{1}{2}.AB.BD.sinB\) các số liệu nêu trên đã có, chỉ cần thế vào là có góc B
Gọi I là tâm. Tìm độ dài bán kình bằng công thức SABD=\(\dfrac{AB.BD.DA}{4AI}\)
ta tìm được độ dài AI còn cách xác định tâm thì dựa vào giao điểm 2 đường thẳng (d) chứa đoạn AI và (d') chứa đoạn BI là xong
Chọn A.
Áp dụng công thức diện tích ta có
Từ giả thiết: a.sinA + b.sinB + c.sinC = ha + hb + hc ta suy ra:
Quy đồng khử mẫu ta được:
2a2 + 2b2 + 2c2 = 2 ab + 2bc + 2ca hay (a - b) 2 + (b - c) 2 + (c - a) 2 = 0
Do đó: a = b = c
Vậy tam giác ABC đều.