Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

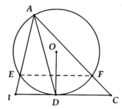
A B C D E F
a)
+) Tứ giác AEDF nội tiếp
=> ^AED = ^DFC (1)
và ^AFD = ^BED ( 2)
+) Ta có: ^EAD = ^FAD ( AD là phân giác ^BAC )
^FDC = ^FAD ( cùng chắn cung DF )
^BDE = ^EAD ( cùng chắn cung DE )
=> ^FDC = ^FAD = ^EAD = ^BDE ( 3)
+) Xét \(\Delta\)AED và \(\Delta\)DFC có:
^EAD = ^FDC ( theo (3))
^AED = ^DFC ( theo (1)
=> \(\Delta\)AED ~ \(\Delta\)DFC
=> \(\frac{AE}{DF}=\frac{ED}{FC}\)=> AE . FC = DF . ED ( 4)
+) Xét \(\Delta\)AFD và \(\Delta\)DEB có:
^DAF = ^BDE ( theo (3))
^AFD = ^DEB ( theo ( 2)
=> \(\Delta\)AFD ~ \(\Delta\)DEB
=> \(\frac{AF}{ED}=\frac{DF}{BE}\Rightarrow AF.BE=DF.ED\)(5)
Từ (4) ; (5) => AF.BE = AE.FC
=> \(\frac{AF}{FC}=\frac{AE}{BE}\)
=> EF//BC
b) Xét \(\Delta\)AED và \(\Delta\)ADC có:
^EAD = ^DAC
^ADE = ^ACD ( vì ^ADE = ^AFE ( chắn cung AE ) và ^AFE = ^ACD (đồng vị ))
=> \(\Delta\)AED ~ \(\Delta\)ADC
=> \(\frac{AE}{AD}=\frac{AD}{AC}\)
=> AD^2 = AE.AC
c) Tương tự cm \(\Delta\)AFD ~ \(\Delta\)ADB
=> \(\frac{AF}{AD}=\frac{AD}{AB}\)
=> AD^2=AF.AB
kết hợp vs câu b => AB.AF = AE.AC

a, HS tự chứng minh
b, ∆ADE:∆ACD (g.g)
=> A D 2 = A E . A C
c, Tương tự: ∆ADF:∆ABD => A D 2 = A B . A F => ĐPCM

Xét 2 tg AED và ADC có
^EAD=^DAC (đề bài) (1)
Ta có:
^AEF=^ADF (Góc nt cùng chắn cung AF)
^DEF= 1/2 số đo cung DF (góc nt)
^CDF=1/2 số đo cung DF (góc giới hạn bởi tiếp tuyến và dây cung)
=> ^AEF+^DEF=^AED=^ADF+^CDF=^ADC (2)
Từ (1) và (2) => tg AED và tg ADC đồng dạng
=> AE/AD=AD/AC => AD^2=AE.AC

Câu hỏi của TRẦN PHAN ĐỨC MINH - Toán lớp 9 - Học toán với OnlineMath

c) *MOHD nội tiếp (cmb) \(\Rightarrow\)^DHB = ^DOM Mà ^DHM +^BHD=180 và ^DOM +^EOD =180 => ^EOD = ^BHD
Mặt khác, ^EOD =^BQD (OM // BQ) => ^BHD = ^BQD => BHQD nội tiếp.
=>đpcm
d) Kéo dài BQ cắt AC tại J
Cm Q là trung điểm BJ (đường trung bình)
Cm \(\frac{EO}{BQ}\)\(=\)\(\frac{OF}{QJ}\)(\(=\)\(\frac{AO}{AQ}\)) \(\Rightarrow\)Đpcm

Câu hỏi của TRẦN PHAN ĐỨC MINH - Toán lớp 9 - Học toán với OnlineMath