
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chứng minh tứ giác AEDF là hình thoi
Þ EF là phân giác của A E D ^
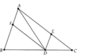

Xét tư giác AEDF có
DF//AE; DE//AF => AEDF là hình bình hành
Gọi O là giao của AD và EF => IA=ID và IE=IF
Xét tg AEFF có
IE=IF => AI là đường trung tuyến của tg AEF
mà AI là phân giác của \(\widehat{BAC}\)
=> tg AEF cân tại A (tg có đường trung tuyến đồng thời là đường phân giác thì tg đó là tg cân) \(\Rightarrow AD\perp EF\) (trong tg cân đường trung tuyến đồng thời là đường cao)
=> AEDF là hình thoi (Hình bh có hai đường chéo vuông góc nhau là hình thoi
=> EA=ED
Xét tg AEI và tg DEI có
EA=ED
IA=ID
EI chung
=> tg AEI=tgDEI (c.c.c) \(\Rightarrow\widehat{AEF}=\widehat{DEF}\) => EF là phân giác của \(\widehat{AED}\)

M A B C E F
Xét ΔABC có MF // AB; BM=CM (gt)
=> AF=CF
Cmtt, ta đc: AE=BE
Do đó EF là đường TB ΔABC
=> EF // BC
Nên BCFE là hình thang (1)
Lại có: ΔABC cân tại A
=> B = C (2)
Từ (1)(2) suy ra BCFE là hình thang cân.
Hình vẽ ko đẹp lắm +_+ thông cảm hen----cx có nhiều cách giải khác nx nha bn
