Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O là giao điểm của 3 đường trung trực của tam giác ABC
⇒ O là tâm đường tròn ngoại tiếp tam giác ABC
OD > OE ⇒ AB < AC

O là giao điểm của 3 đường trung trực của tam giác ABC
⇒ O là tâm đường tròn ngoại tiếp tam giác ABC
a) OE = OF ⇒ AC = BC
b) OD > OE ⇒ AB < AC

O là giao điểm của 3 đường trung trực của tam giác ABC
⇒ O là tâm đường tròn ngoại tiếp tam giác ABC
OD > OE ⇒ AB < AC

Gọi M,N,IM,N,I lần lượt là trung điểm AB,AC,ADAB,AC,AD
có M,N,IM,N,I thẳng hàng
AIEMAIEM nội tiếp⇒ˆAEF=ˆAMN⇒AEF^=AMN^(1)
AINFAINF nội tiếp ⇒ˆAFE=ˆANM⇒AFE^=ANM^(2)
(1,2)⇒ˆEDF=ˆEAF=90∘=ˆEOF⇒EDF^=EAF^=90∘=EOF^
⇒A,O,D,E,F⇒A,O,D,E,F cùng thuộc 1 đường tròn
b)
có △AEF△AEF luôn đồng dạng với △AMN△AMN cố định
⇒SAEF⇒SAEFmin khi AEAE min
có AE≥AMAE≥AM
⇒SAEF⇒SAEF min khi E≡M,F≡NE≡M,F≡N
lúc đó SAEF=bc8SAEF=bc8

Kẻ IG⊥AB tại G, kẻ IK⊥AC tại K
Xét ΔCKI vuông tại K và ΔCDI vuông tại D có
CI chung
\(\hat{KCI}=\hat{DCI}\)
Do đó: ΔCKI=ΔCDI
=>CK=CD và IK=ID
Xét ΔBGI vuông tại G và ΔBDI vuông tại D có
BI chung
\(\hat{GBI}=\hat{DBI}\)
Do đó: ΔBGI=ΔBDI
=>BG=BD
Xét ΔAKI vuông tại K và ΔAGI vuông tại G có
AI chung
\(\hat{KAI}=\hat{GAI}\)
Do đó: ΔAKI=ΔAGI
=>AK=AG
\(\frac{a+b-c}{2}=\frac{BC+AC-AB}{2}\)
\(=\frac{BD+CD+CK+KA-AG-GB}{2}=\frac{BD-BG+CD+CK+KA-AG}{2}\)
\(=\frac{CD+CK}{2}=\frac{2\cdot CD}{2}=CD\)
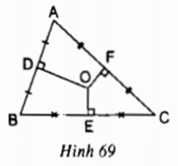
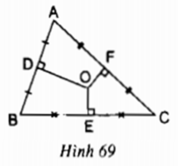
O là giao điểm của 3 đường trung trực của tam giác ABC
⇒ O là tâm đường tròn ngoại tiếp tam giác ABC
OE = OF ⇒ AC = BC