Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
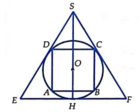
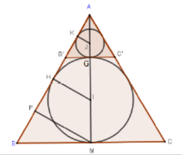
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ SEF đều” (hình vẽ).
![]()
=>Bán kính đáy và chiều cao của hình trụ (T) lần lượt là
![]()
và ![]()
Thể tích khối trụ là
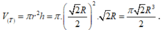
Ta có ∆ SEF đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của ∆ SEF.
Gọi H là trung điểm của EF thì
Hình vuông ABCD nội tiếp đường tròn (O) nên SH = 3OH = 3R![]()
Bán kính đáy và chiều cao của hình nón (N) lần lượt là ![]()
Thể tích khối nón là
![]()

Chọn đáp án A
Đường tròn (S; R) có
+ Chu vi hình tròn (S; R) là C = 4 π
+ Diện tích hình tròn (S; R) là S = 4 π . Khi cắt 1 4 hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón, ta có. Diện tích xung quanh hình nón là
![]()
Chu vi đáy của hình nón là
![]()
bán kính đáy của hình nón là r = 3 2
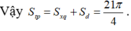

Đáp án B
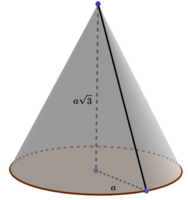
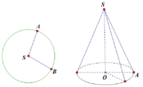
Dễ có chu vi của đáy là hình tròn bằng: p = π d = 2 π a
Khoảng cách từ đỉnh đến một điểm thuộc vành của hình nón bằng:
SA = ![]()
Suy ra diện tích xung quanh hình nón là diện tích hình quạt có bán kính 2a và độ dài cung là 2 π a. Ta dễ tính được chu vi của hình tròn bán kinh 2a là 4 π a. Do đó diện tích hình quạt cần tính bằng nửa hình tròn này. Từ đây ta thu được kết quả: S x q = 2 πa 2 => Chọn đáp án B.

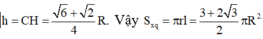



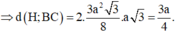
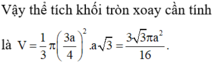



Đáp án B
Áp dụng định lý hàm số sin, ta có
Lai có:
Khi quay ∆ ABC quanh AC thì ∆ BHC tạo thành hình nón tròn xoay (N) có đường sinh
bán kính đáy
Diện tích xung quanh hình nón (N) là: