Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có ^AIC' = ^IAC + ^ICA = ^IAB + ^ICB = ^IAB + ^BAC' = ^IAC' => \(\Delta\)AC'I cân tại C'
=> C' nằm trên trung trực của AI. Tương tự B' cũng nằm trên trung trực của AI => B'C' vuông góc AI
Hay A'I vuông góc với B'C'. Lập luận tương tự B'I vuông góc A'C', C'I vuông góc A'B'
Do đó I là trực tâm của \(\Delta\)A'B'C' (đpcm).
b) Ta thấy ^FDE = ^A'DC' = ^A'AC' = ^IAC' = C'IA (Vì \(\Delta\)AC'I cân tại C') = ^EIC'
Suy ra tứ giác DEIF nội tiếp (đpcm).
c) Gọi S là tâm ngoại tiếp của \(\Delta\)DEF. Vì tứ giác DEIF nội tiếp (cmt) nên S đồng thời là tâm ngoại tiếp DEIF
Gọi giao điểm thứ hai giữa (S) và (O) là G. Khi đó ^DFG = ^DEG => ^GFA' = ^GEC'
Lại có ^EGF = ^EDF = ^A'DC' = ^A'GC' => ^FGA' = ^EGC'. Do vậy \(\Delta\)GEC' ~ \(\Delta\)GFA' (g.g)
=> \(\frac{GC'}{GA'}=\frac{EC'}{FA'}\). Mặt khác ^A'IF = ^C'IA = ^C'AI = ^C'AE và ^IA'F = ^AA'D = ^AC'D = ^AC'E
Cho nên \(\Delta\)AEC' ~ \(\Delta\)IFA' (g.g) => \(\frac{EC'}{FA'}=\frac{AC'}{IA'}\). Mà các điểm A,I,A',C' đều cố định
Nên tỉ số \(\frac{AC'}{FA'}\) là bất biến. Như vậy \(\frac{GC'}{GA'}\)không đổi, khi đó tỉ số giữa (GC' và (GA' của (O) không đổi
Kết hợp với (O), A',C' cố định suy ra G là điểm cố định. Theo đó trung trực của IG cố định
Mà S thuộc trung trực của IG (do D,I,E,F,G cùng thuộc (S)) nên S di động trên trung trực của IG cố định (đpcm).


![]() (hai góc đối đỉnh)
(hai góc đối đỉnh)
![]()
![]()
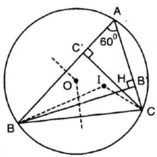
⇒ B, O, I, H, C cùng thuộc đường tròn chứa cung 120º dựng trên đoạn BC.

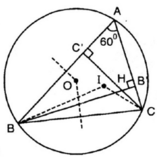

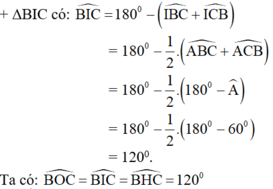
⇒ B, O, I, H, C cùng thuộc đường tròn chứa cung 120º dựng trên đoạn BC.
Kiến thức áp dụng
+ Các điểm cùng nhìn một đoạn thẳng cố định dưới cùng một góc α thì đều thuộc cùng một đường tròn.