Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn phương án (B)
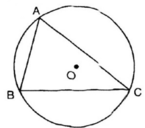
Tam giác đều ABC nội tiếp đường tròn tâm O bán kính R. Khi đó \(\widehat{BOC}\) có số đo bằng \(120^0\)
Các cung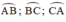 
tạo thành một đường tròn
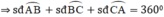
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
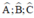là các góc nội tiếp chắn các cung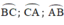 
Vậy chọn đáp án C.
A B C O J I N H M P
Gọi P ; M lần lượt là giao điểm của CH và BH với AB và AC
a) Ta có:^CPA = ^BMA = 90o => ^HPA = ^HMA = 90o => ^HPA + ^HMA = 180o
=> Tứ giác HPAM nội tiếp
=> ^PAM + ^PHM = 180o
=> ^BHC = ^PHM = 180o - ^PAM =180o - \(\alpha\)
b) I là tâm đường tròn ngoại tiếp \(\Delta\)HBC
=> IB = IH = IC
=> \(\Delta\)IBH và \(\Delta\)IIHC cân tại I
=> ^IBH = ^IHB và ^ICH = ^IHC
=> ^IBH + ^ICH = ^IHB + ^IHC = ^BHC = \(180^o-\alpha\)
=> ^BIC = 360o - ^IBH - ^ICH - ^BHC = \(2\alpha\)
Ta lại có ^BOC = 2.^BAC = \(2\alpha\) ( góc ở tâm và góc nội tiếp cùng chắn cung BC)
=> ^BIC = ^BOC (1)
Mặt khác: OB = OC; IB = IC
=> OI là đường trung trực của BC (2)
Từ (1) ; (2) => O; I nằm khác phía so với BC
Mà \(\Delta\)BIC cân => IO là đường phân giác ^BIC
=> OIC = \(\frac{1}{2}\).^BIC = \(\alpha\)
c) Từ (b) => ^BIO = ^CIO = ^BOI = ^COI
=> BOCI là hình bình hành có OI vuông BC
=> BOCI là hình thoi
mà B; C; O cố định => I cố định
Tương tự ta cungc chứng minh được: OCJA là hình thoi
=> CJ = CO = R mà C; O cố định
=> J nằm trên đường tròn tâm C bán kính R cố định
d) AJCO là hình thoi => AJ // = OC
OCIB là hình thoi => OC // = BI
=> AJ //=BI
=> AJIB là hình bình hành có hai đường chéo AI; BJ cắt nhau tại N
=> N là trung điểm của AI
Chọn phương án (B)
Hình vuông XYZT nội tiếp đường tròn tâm O bán kính R. Điểm M bất kì thuộc cung XT. \(\widehat{ZMT}\) có số đo bằng \(45^0\)
Các cung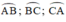 
tạo thành một đường tròn
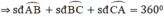
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
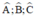là các góc nội tiếp chắn các cung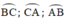 
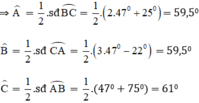
Vậy chọn đáp án C.
Hướng dẫn làm bài:
Vì các cung AB, BC, CA tạo thành đường tròn, do đó:
(x + 75°) + (2x + 25°) + (3x - 22°) = 360°
⇔ 6x + 78° = 360° ⇔ 6x = 282° ⇔ x = 47°
Vậy sđ cung AB = x + 75° = 47° + 75° = 122°
⇒ˆC=12202=610⇒C^=12202=610
sđ cung BC = 2x + 25° = 2.47° + 25° = 119° ⇒ˆA=11902=59,50⇒A^=11902=59,50
sđ cung AC = 3x - 22° = 3.47° - 22° = 119° ⇒ˆB=11902=59,50⇒B^=11902=59,50
Chọn đáp án C