Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
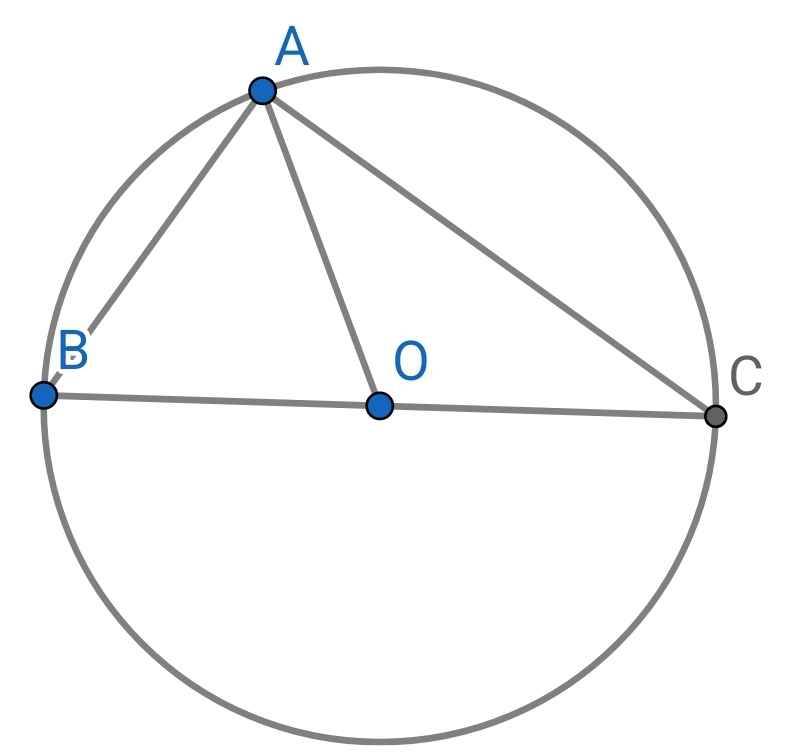Cách 1: Dùng tính chất đường trung tuyến AO bằng nửa cạnh BC
Ta có:
OA = OB = OC = bán kính
⇒ OA = BC : 2
⇒ ∆ABC vuông tại A
⇒ ∠BAC = 90⁰
Cách 2: Dùng định lí
Do ∆ABC nội tiếp (O) đường kính BC
⇒ ∆ABC vuông tại A
⇒ ∠BAC = 90⁰
Chọn đáp án A
Tổng số đo 3 góc của 1 tam giác bằng 180° nên :
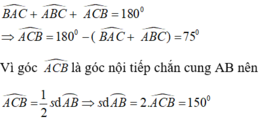
a)
Theo tính chất đường phân giác áp dụng cho \(\Delta ABC\) có BD là phân giác góc ABC \(\Rightarrow\frac{AB}{BC}=\frac{AD}{DC}=\frac{1}{2}\)
\(\Delta ABC\) vuông tại A\(\Rightarrow\tan B=\frac{AB}{BC}=\frac{1}{2}\Rightarrow\widehat{B}\approx27\)
b,
Thấy \(\widehat{ACB}\) nội tiếp \(\left(O\right)\) chắn cung AB nhỏ
\(\Rightarrow\widehat{ACB}=\frac{1}{2}sđ\overline{AB}\left(1\right)\)
Thấy \(\widehat{AOB}\) chắn cung AB nhỏ \(\Rightarrow\widehat{AOB}=sđ\overline{AB}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{AOB}=2\widehat{ACB}=2\left(180^o-70^o-60^o\right)=2.50^o=100^o\)
khi tia OA cắt đường tròn tâm O tại D nên AD là đường kính chia ra 2 cung AD bằng nhau
mà tam giác ABC cân tại A có góc ABC =góc ACB là 2 góc nội tiếp chắc 2 cung AB và AC nên cung AB=cung AC
cung AD=cung AB+cung BD
cung AD=cung AC+cung CD
ta có cung AD=cung AD,cung AB=AC=>cung BD=cung CD
theo đề bài số đo cung nhỏ BD=cung BD+cung CD=>100=2 cung CD=>cung CD bằng 50 độ
MÀ GÓC COD là góc ở tâm chắc cung CD
NÊN SUY RA ĐƯỢC GÓC COD BẰNG 50 ĐỘ
Các cung 
tạo thành một đường tròn
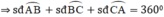
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
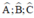là các góc nội tiếp chắn các cung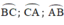 
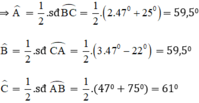
Vậy chọn đáp án C.
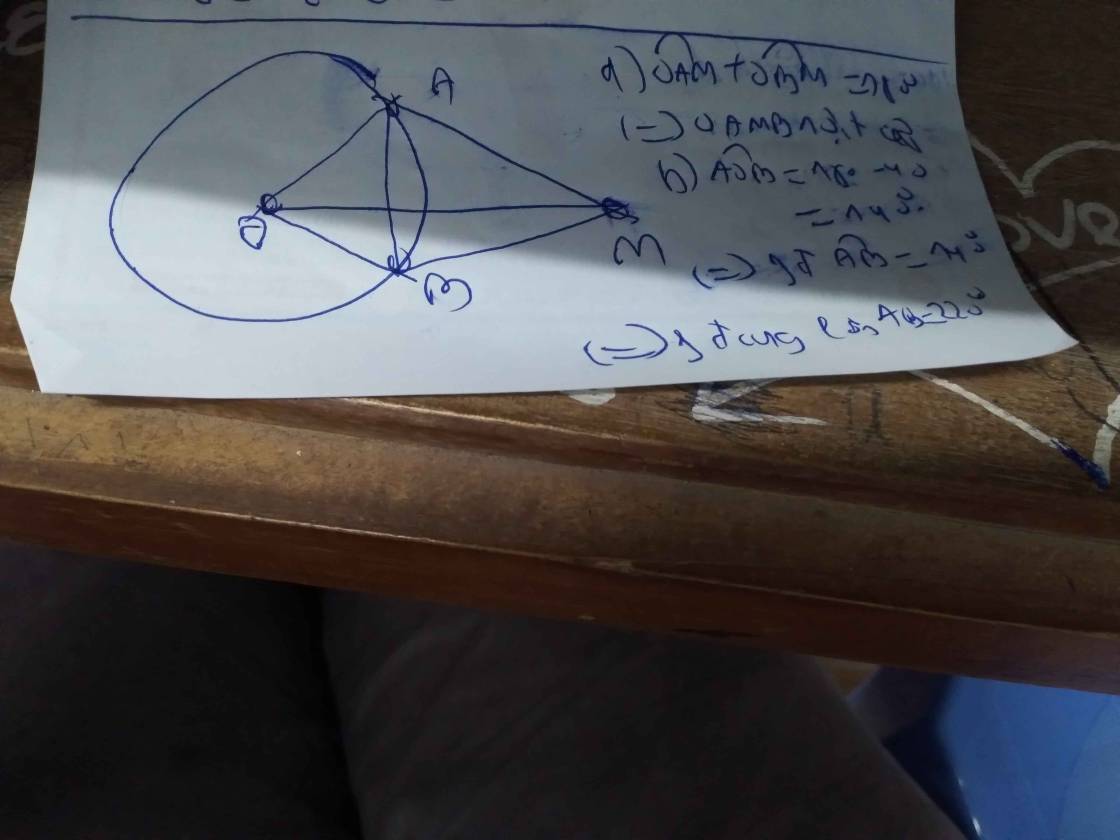
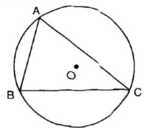
\(\widehat{AOB}=2\widehat{C}=120^0\) (góc ở tâm gấp đôi góc nội tiếp cùng chắn cung AB)
Xét $(O)$ có: $\widehat{AOB}=2.\widehat{ACB}$ (góc ở tâm và góc nội tiếp cùng chắn cung $AB$)
suy ra $\widehat{AOB}=2.\widehat{ACB}=2.60^o=120^o$