Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) ACB=60 =>ACO đều => S ACO = 5 căn 3
S hình quạt AOC=(pi*5^2*60)/180
d) vì BC không đổi => S ABC max khi đường cao hạ từ A max => khi A chính giữa nữa dg tròn

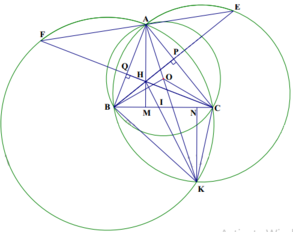
Gọi (O’) là đường tròn đi qua bốn điểm B, H,C, K. Ta có dây cung B C = R 3
BKC=60o= BAC nên bán kính đường tròn (O’) bằng bán kính R của đường tròn (O).
Gọi M là giao điểm của AH và BC thì MH vuông góc với BC, kẻ KN vuông góc với BC (N thuộc BC), gọi I là giao điểm của HK và BC.
Bài giảng học thử

a: Kẻ BD vuông góc AC,CE vuông góc AB
góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc AED=góc ACB
=>ΔAED đồng dạng vơi ΔACB
Tâm M của đường tròn ngoại tiếp tứ giác BDCE là trung điểm của BC
Gọi H là giao của BD và CE
=>AH vuông góc BC tại N
Gọi giao của OM với (O) là A'
ΔOBC cân tại O
=>OM vuông góc BC
AN<=A'M ko đổi
=>\(S_{ABC}=\dfrac{1}{2}\cdot AN\cdot BC< =\dfrac{1}{2}\cdot A'M\cdot BC_{kođổi}\)
Dấu = xảy ra khi A trùng A'
=>A là điểm chính giữa của cung BC
a: góc BOC=2*góc A=90 độ
=>OB^2+OC^2=BC^2
=>2*R^2=2^2=4
=>R=căn 2
\(S_{\left(O\right)}=R^2\cdot pi=2pi\left(cm^2\right)\)
b: \(S_{q\left(BOC\right)}=pi\cdot2\cdot\dfrac{90}{360}=\dfrac{1}{2}\cdot pi\left(cm^2\right)\)
\(S_{BOC}=\dfrac{1}{2}\cdot OB\cdot OC=\dfrac{1}{2}\cdot2=1\)
=>\(S_{viênphân}=\dfrac{1}{2}\cdot3.14-1=0.57\left(cm^2\right)\)
Ko có hình vẽ với phần c ạ