Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ đường kính AK
+) Dễ có: ^KBC = ^KAC (2 góc nội tiếp cùng chắn cung KC) (1)
+) ^ABK là góc nội tiếp chắn nửa đường tròn nên ^ABK = 900
Có: ^KBC + ^CBA = ^ABK = 900 (cmt)
^BAH + ^CBA = 900 (∆ABH vuông tại H)
Từ đó suy ra ^KBC = ^BAH (2)
Từ (1) và (2) suy ra ^BAH = ^KAC hay ^BAH = ^OAC (đpcm)
Kẻ đường kính AE của đường tròn ( O) . Ta thấy \(\widehat{ACE}=90^o\)( góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow\widehat{OAC}+\widehat{AEC}=90^o\) (1)
Theo gt, ta có: \(\widehat{BAH}+\widehat{ABC}=90^O\) (2)
Lại có: \(\widehat{AEC}=\widehat{ABC}\) (3)
Từ (1), (2), (3) => đpcm

a) Xét (O) có :
AB là tiếp tuyến tại B
AC là tiếp tuyến tại C
AB cắt AC tại A
\(\Rightarrow\widehat{ABO}=\widehat{ACO}=90^o\)và OA là p/g \(\widehat{BOC}\)
Xét tg ABOC có \(\widehat{ABO}+\widehat{ACO}=180^o\)Mà 2 góc này đối nhau
\(\Rightarrow\)ABOC là tg nt
b) Xét (O) có
\(\widehat{ABE}\)là góc tạo bởi tiếp tuyến AB và dây BE
\(\widehat{BDE}\)là góc nt chắn cung BE
\(\Rightarrow\widehat{ABE}=\widehat{BDE}=\frac{1}{2}sđ\widebat{BE}\)
Xét \(\Delta ABEvà\Delta ADB:\)
\(\widehat{BAD}\)chung
\(\widehat{ABE}=\widehat{BDE}\)
\(\Rightarrow\Delta ABE\infty\Delta ADB\left(gg\right)\)
\(\Rightarrow\frac{AB}{AD}=\frac{AE}{AB}\Rightarrow AB^2=AD.AE\)
c) Vì OA là p/g \(\widehat{BOC}\Rightarrow\widehat{BOA}=\widehat{COA}=\frac{\widehat{BOC}}{2}\)
Do ABOC là tg nt\(\Rightarrow\widehat{BOA}=\widehat{BCA}\)(cùng chắn cung AB)
Suy ra \(\widehat{AOC}=\widehat{ACB}\)

Vẽ đường kính CM
\(MA\perp AC\)(\(\Delta MAC\)nội tiếp)
\(BE\perp AC\)(giả thiết)
\(\Rightarrow\)\(MA//BH\) (1)
\(MB\perp BC\)(\(\Delta MBC\)nội tiếp)
\(AH\perp BC\)(giả thiết)
\(\Rightarrow\)\(MB//AH\)(2)
Từ (1)(2):
\(\Rightarrow\)\(MAHB\)là hình bình hành.
\(\Rightarrow\)\(AH=BM\)
Do\(\widehat{BAC}=60^0\)
\(\Rightarrow BC=R\sqrt{3}\)
Áp dụng địn lí Pytago vào \(\Delta BMC\)
\(BM^2+BC^2=MC^2\)
\(\Leftrightarrow\)\(BM^2=4R^2-3R^2\)
\(\Leftrightarrow\)\(BM^2=R^2\)
\(\Leftrightarrow\)\(BM=\sqrt{R^2}=R\)
\(\Rightarrow\)\(AH=BM=R\)
Mà \(AO=\frac{2R}{2}=R\)
\(\Rightarrow\)\(AH=AO\)
\(\Rightarrow\)\(\Delta AHO\)cân tại \(A\)(ĐPCM)

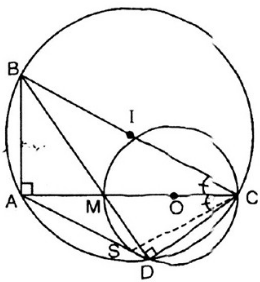
a, ta có ^BAC=900(góc nội tiếp chắn nửa đường tròn đường kính BC)
^MDC=900(góc nội tiếp chắn nửa đường tròn đường kính MC)
=>^BAC=^MDC(=900)
=>tứ giác ABCD nội tiếp (hai đỉnh A và D kề nhau cùng nhìn cạnh BC dưới hai góc bằng nhau)
b. vì tứ giác ABCD nội tiếp (câu a) nên ^ABD=^ACD (hai góc nội tiếp cùng chắn cung AD)
c, ta có bốn điểm D,S,C,M cùng thuộc đường tròn đường kính MC
=>tứ giác DSCM nội tiếp
=>^ADM=^SCM (cùng bù với ^MDS)
Mà ADCB nội tiếp nên ^ADM=^MCB( hai góc nội tiếp cùng chắn cung AB)
Do đó ^SCM=^MCB
=>CA là tia phân giác ^SCB

a) Ta có: AM là phân giác \(\widehat{BAC}\)=> \(\widehat{BAM}\)= \(\widehat{CAM}\)=> \(\widebat{BM}\)=\(\widebat{CM}\)
=> BM = CM
mà OB=OC (bán kính (O))
=> OM là đường trung trực của BC => OM đi qua tđ N của BC
b) Từ A vẽ đường kính AQ => tam giác ACQ vuông tại C => \(\widehat{CAO}\)+ \(\widehat{AMC}\)=90 (1)
AK là đg cao => tam giác AKB vuông tại K => \(\widehat{BAK}\)+ \(\widehat{ABK}\)=90 (2)
mà \(\widehat{AMC}\)= \(\widehat{ABK}\)(cùng chắn \(\widebat{AC}\)) (3)
Từ (1),(2),(3) => \(\widehat{CAO}\)= \(\widehat{BAK}\)
mà \(\widehat{BAM}\)= \(\widehat{MAC}\)(cmt)
\(\widehat{BAM}\)= \(\widehat{BAK}\)+ \(\widehat{KAM}\)
\(\widehat{MAC}\)= \(\widehat{CAO}\)+\(\widehat{MAO}\)
=> \(\widehat{KAM}\)= \(\widehat{MAO}\)

Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{ADC}\)(Hệ quả góc nội tiếp)
hay \(\widehat{ABH}=\widehat{ADC}\)(1)
Xét (O) có
ΔADC nội tiếp đường tròn(A,D,C∈(O))
AD là đường kính(gt)
Do đó: ΔADC vuông tại C(Định lí)
Suy ra: \(\widehat{DAC}+\widehat{ADC}=90^0\)(Hai góc nhọn phụ nhau)(2)
Ta có: ΔABH vuông tại H(AH⊥BC)
nên \(\widehat{BAH}+\widehat{ABH}=90^0\)(Hai góc nhọn phụ nhau)(2)
Từ (1) và (2) suy ra \(\widehat{BAH}=\widehat{DAC}\)(đpcm)