Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O A B C D K
Kẽ OA cắt đường tròn tại D cắt BC tại K
Ta có OA = OB = OD = R
\(\Rightarrow\)\(\Delta ABD\) vuông tại D
\(\Rightarrow BD=\sqrt{OD^2-AB^2}=\sqrt{10^2-8^2}=6\)
Ta có OK là đường trung trực của BC nên \(\hept{\begin{cases}OK⊥BC\\BK=CK\end{cases}}\)
Ta lại có: \(S_{\Delta ABD}=\frac{1}{2}AB.BD=\frac{1}{2}AD.BK\)
\(\Rightarrow BK=\frac{AB.BD}{AD}=\frac{8.6}{10}=4,8\)
\(\Rightarrow BC=2BK=4,8.2=9,6\)
Viết nhầm tùm lum hết. Do không thấy cái hình. Mà thôi nhìn hình sửa hộ luôn nhé

A B C 0 H D
Vẽ đường kính AD và AH⊥BC(H∈BC)AH⊥BC(H∈BC).
Ta có \(\widehat{ACD}\)ACD^ là góc nội tiếp chắn nửa đường tròn ⇒\(\widehat{ACD}\)=900⇒ACD^=900.
Xét ΔABHΔABH và ΔADCΔADC có:
\(\widehat{AHB}\)=\(\widehat{ACD}\)=900AHB^=ACD^=900;
ABH^=ADC^ \(\widehat{ABH}=\widehat{ADC}\)(hai góc nội tiếp cùng chắn cung AC);
⇒ΔABH∼ΔADC(g.g)⇒AHAC=ABAD⇒515=82R⇒2R=24⇔R=12(c

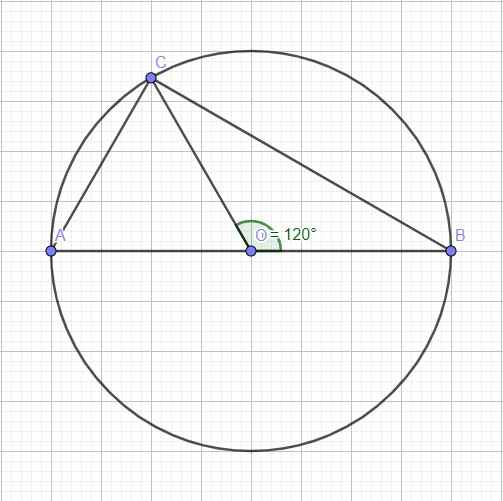
Do AB là đường kính \(\Rightarrow\widehat{ACB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\) Tam giác ABC vuông tại C
Mặt khác \(OA=OC=R\Rightarrow\Delta OAC\) cân tại O (1)
\(\widehat{AOC}=180^0-\widehat{BOC}=60^0\) (2)
(1);(2) \(\Rightarrow\Delta AOC\) đều \(\Rightarrow AC=OA=R\)
Áp dụng Pitago:
\(BC=\sqrt{AB^2-AC^2}=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)

ABC vuông tại A
Gọi r là bán kính ; các tiếp điểm AC ;AB ;BC la M;N;P
=> AN = AM =r
=> BN =BP =AB - r = 4- r ; CM =CP =AC-r = 3 -r
Mà BP + PC =BC => 4-r + 3 -r =5 => 2r =2 => r =1

Xét ΔABC vuông tại A có AH ⊥ BC.
⇒ AH² = CH . BH (Hệ thức lượng trong tam giác vuông)
⇒ BH = AH² : CH
⇒ BH = 10² : 5
⇒ BH = 100 : 5
⇒ BH = 20 (cm)
Ta có: BC = BH + CH = 20 +5 = 25 (cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=BH\cdot CH\)
\(\Leftrightarrow BH=10^2:5=20\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=20+5=25(cm)

Lời giải:
$\widehat{BAC}$ nhìn cạnh $BC$, mà $BC$ là đường kính nên:
$\widehat{BAC}=90^0$ (góc nội tiếp chắn nửa đường tròn)
$\Rightarrow \triangle ABC$ vuông tại $A$
$AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-5^2}=5\sqrt{3}$ (theo định lý Pitago)
$AH=\frac{AB.AC}{BC}=\frac{5.5\sqrt{3}}{10}=2,5\sqrt{3}$ (cm)