Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có BOC=120o ;BKC =60o suy ra BOC +BKC =1800 nên tứ giác BOCK nội tiếp đường tròn.
Ta có OB=OC=R suy ra OB= OC=> BKO= CKO hay KO là phân giác góc BKC theo phần (a) KA


a) Do AB // DE nên \(\widebat{AE}=\widebat{BD}\Rightarrow\widebat{AE}+\widebat{DC}=\widebat{BD}+\widebat{DC}=\widebat{BC}\)
Ta có \(\widehat{MIC}\) là góc có đỉnh nằm trong đường tròn nên \(\widehat{MIC}=\frac{\widebat{AE}+\widebat{DC}}{2}=\frac{\widebat{BC}}{2}\)
Góc \(\widehat{MBC}\) là góc tạo bởi tiếp tuyến và dây cung nên \(\widehat{MBC}=\frac{\widebat{BC}}{2}\)
Suy ra \(\widehat{MIC}=\widehat{MBC}\)
Xét tứ giác BMCI có \(\widehat{MIC}=\widehat{MBC}\) nên BMCI là tứ giác nội tiếp.
b) Ta có \(\widehat{MIC}=\widehat{MBC}\Rightarrow\Delta FIC\sim\Delta FBM\left(g-g\right)\)
\(\Rightarrow\frac{FI}{FB}=\frac{FC}{FM}\Rightarrow FI.FM=FB.FC\)
Ta cũng có \(\widehat{DBF}=\widehat{CEF}\Rightarrow\Delta BFD\sim\Delta EFC\left(g-g\right)\)
\(\Rightarrow\frac{FB}{FE}=\frac{FD}{FC}\Rightarrow FE.FD=FB.FC\)
Vậy nên \(FI.FM=FE.FD\)
c) Do PQ là đường kính nên \(\widehat{PTQ}=90^o\)
Suy ra \(\Delta FIQ\sim\Delta FTM\left(c-g-c\right)\Rightarrow\widehat{FTM}=\widehat{FIQ}\)
Lại có BIMC nội tiếp, BOCM cũng nội tiếp nên 5 điểm B, O, I, C, M cùng thuộc đường trong đường kính OM.
Suy ra \(\widehat{FIQ}=90^o\)
Vậy thì P, T, M thẳng hàng.
d) Ta thấy \(S_{IBC}=\frac{1}{2}BC.d\left(I,BC\right)\)
Do BC không đổi nên SIBC lớn nhất khi d(I; BC) lớn nhất.
Điều này xảy ra khi I trùng O hay tam giác ABC vuông tại B.
Vậy diện tích tam giác IBC lớn nhất khi AC là đường kính đường tròn (O).

A B C D E F O I J M P Q L K T
a) Vì tứ giác BFEC nội tiếp nên \(\widehat{PFB}=\widehat{ACB}=\widehat{PBF}\) suy ra \(PF=PB\)
Suy ra \(MP\perp AB\) vì MP là trung trực của BF. Do đó \(MP||CF\). Tương tự \(MQ||BE\)
b) Dễ thấy M,I,J đều nằm trên trung trực của EF cho nên chúng thẳng hàng. Vậy IJ luôn đi qua M cố định.
c) Gọi FK cắt AD tại T ta có \(FK\perp AD\) tại T. Theo hệ thức lượng \(IE^2=IF^2=IT.IL\)
Suy ra \(\Delta TIE~\Delta EIL\). Lại dễ có \(EI\perp EM\), suy ra ITKE nội tiếp
Do vậy \(\widehat{ILE}=\widehat{IET}=\widehat{IKT}=90^0-\widehat{LIK}\). Vậy \(IK\perp EL.\)

A B C I E F O H K
Gọi IE,IF cắt đường tròn (O) lần thứ hai lần lượt tại H,K. Lúc đó ta có ^BIH = ^CIK = 900
=> ^BIH và ^CIK chắn nửa đường tròn (O) => BH,CK là các đường kính của (O)
Xét bộ 6 điểm A,B,C,H,I,K cùng nằm trên (O): BH cắt CK tại O, IH cắt AC tại E, IK cắt AB tại F
Suy ra 3 điểm E,O,F thẳng hàng (ĐL Pascal). Hay EF đi qua O cố định (đpcm).
P/S: Định lí Pascal khá nổi tiếng, bạn có thể tham khảo cách chứng minh trong các sách nâng cao (NC&PT Toán 9 tập 2).
A B C O F E K S P D Q M S'
a) Ta sẽ chứng minh SK đi qua điểm O cố định. Thật vậy, gọi OK cắt AP tại S', ta cần chứng minh S' trùng với S.
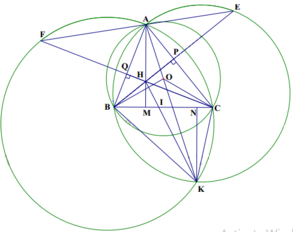
Ta có: ^CKF + ^BAC = ^CKF + ^CPE = ^CKF + ^CKE = 1800 => 3 điểm E,K,F thẳng hàng
Thấy ^FPE + ^PEF + ^PFE = ^BPC + ^PBK + ^CPK = ^OBP + ^OCP + ^PBK + ^CPK = ^OBK + ^OCK = 1800
=> Tứ giác BOCK nội tiếp. Mà OB = OC => ^BKO = ^CKO. Lại có: ^DKB = ^AEB = ^PKC
Suy ra: ^BKO - ^DKB = ^CKO - ^PKC => ^AKO = ^OKP
Mặt khác: ^AOK = ^AOB + ^BOK = 2.^ACB + ^BCK = ^ACK + ^ACB = ^BPK + ^APB = ^APK
=> Tứ giác AOPK nội tiếp => ^OAP = ^OKP => ^OAS' = ^OKA (Vì ^AKO = ^OKP)
=> \(\Delta\)OAS' ~ \(\Delta\)OKA (g.g) => OA2 = OS'.OK => OB2 = OS'.OK => \(\Delta\)OS'B ~ \(\Delta\)OBK (c.g.c)
=> ^OS'B = ^OBK. Tương tự: ^OS'C = ^OCK. Do đó: ^OS'B + ^OS'C = ^OBK + ^OCK = 1800 (Vì tứ giác BOCK nội tiếp)
=> 3 điểm B,S',C thẳng hàng => BC cắt AP tại S'. Vậy nên S trùng S' => 3 điểm O,S,K thẳng hàng => ĐPCM.
b) Từ câu a ta có: OD2 = OS.OK => \(\Delta\)ODS ~ \(\Delta\)OKD (c.g.c) => ^ODS = ^OKD = ^OKA = ^OAS
=> Tứ giác AOSD nội tiếp hay 4 điểm A,O,P,S cùng thuộc 1 đường tròn (1)
Ta lại có: ^CAP + ^PAD = ^CAD = ^CBD = ^BMD + ^BDM = ^SMD + ^BDQ = ^SMD + ^BAQ
Mà ^CAP = ^BAQ (gt) nên ^PAD = ^SMD hay ^SMD = ^SAD => 4 điểm A,S,D,M cùng thuộc 1 đường tròn (2)
Từ (1);(2) => 5 điểm A,O,S,P,M cùng thuộc 1 đường tròn. Do OA = OD nên ^AMO = ^DMO hay ^AMO = ^QMO
Xét \(\Delta\)AOQ cân tại O, một điểm M sao cho ^AMO = ^QMO (cmt). Dễ c/m AM = QM (Gợi ý: Lấy đối xứng của M qua OA)
Từ đó: OM là trung trực của AQ => OM vuông góc AQ (đpcm).