Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .

1). Tam giác ABF và tam giác ACE ần lượt cân tại F, E và
F B A ^ = E C A ^ = A ^ 2 ⇒ Δ A B F ∽ Δ A C E .
2). Giả sử G là giao điểm của BE và CF.
Ta có G F G C = B F C E = A B A C = D B D C ⇒ G D ∥ F B , và F B ∥ A D ta có G ∈ A D .
3). Chứng minh B Q G ^ = Q G A ^ = G A E ^ = G A C ^ + C A E ^ = G A B ^ + B A F ^ = G A F ^ , nên AGQF nội tiếp, và Q P G ^ = G C E ^ = G F Q ^ , suy ra tứ giác FQGP nội tiếp.
1) Chứng minh rằng tam giác \( A B F \) đồng dạng với tam giác \( A C E \):
- Tam giác \(ABF\) và \(ACE\) có:
+ Góc \(A\) chung.
+ Góc \(BAF\) bằng góc \(CAE\) (vì \(AD\) là phân giác của góc \(BAC\) và \(CF\), \(BE\) song song với \(AD\)).
Do đó, tam giác \(ABF\) đồng dạng với tam giác \(ACE\) (theo trường hợp góc-góc).
2) Chứng minh rằng các đường thẳng \(BE\), \(CF\), \(AD\) đồng quy:
- Gọi \(G\) là giao điểm của \(BE\) và \(CF\).
- \(AD\) là phân giác góc \(BAC\), và \(BE\), \(CF\) song song với \(AD\). Do đó, \(G\) cũng nằm trên phân giác \(AD\).
- Vậy \(BE\), \(CF\), \(AD\) đồng quy tại \(G\).
3) Chứng minh rằng các điểm \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn:
- Gọi đường tròn ngoại tiếp tam giác \(GEC\) là \(\omega\).
- \(QE\) cắt \(\omega\) tại \(P\) khác \(E\), vậy \(P\) nằm trên đường tròn \(\omega\).
- \(GQ\) song song với \(AE\), và \(AE\) là đường kính của \(\omega\) (vì \(E\) là trung điểm của \(AC\) và \(G\) nằm trên phân giác của \(BAC\)). Do đó, \(GQ\) là dây cung của \(\omega\).
- \(PF\) là tiếp tuyến của \(\omega\) tại \(P\) (vì \(QE\) là tiếp tuyến và \(PF\) là phần kéo dài của \(QE\)).
- Góc \(PGF\) bằng góc \(GAC\) (cùng chắn cung \(GC\) của \(\omega\)).
- \(AF\) là trung trực của \(AB\), nên \(ABF\) là tam giác cân tại \(A\). Do đó, góc \(AFB\) bằng góc \(ABF\).
- Góc \(ABF\) bằng góc \(GAC\) (do đồng dạng của tam giác \(ABF\) và \(ACE\)).
- Vậy, góc \(PGF\) bằng góc \(AFB\). Do đó, \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn.

A B C D O M N E F
a) Giả sử \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}-\overrightarrow{OD}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{BO}+\overrightarrow{OC}+\overrightarrow{DO}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{BO}+\overrightarrow{OA}\right)+\left(\overrightarrow{DO}+\overrightarrow{OC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\) (đúng do tứ giác ABCD là hình bình hành).
b) \(\overrightarrow{ME}+\overrightarrow{FN}=\overrightarrow{MA}+\overrightarrow{AE}+\overrightarrow{FC}+\overrightarrow{CN}\)
\(=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\).
Do các tứ giác AMOE, MOFB, OFCN, EOND cũng là các hình bình hành.
Vì vậy \(\overrightarrow{CN}=\overrightarrow{FO}=\overrightarrow{BM};\overrightarrow{FC}=\overrightarrow{ON}=\overrightarrow{ED}\).
Do đó: \(\overrightarrow{ME}+\overrightarrow{FN}=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\)
\(=\left(\overrightarrow{MA}+\overrightarrow{BM}\right)+\left(\overrightarrow{AE}+\overrightarrow{ED}\right)\)
\(=\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{BD}\) (Đpcm).

A B C D O M
a) BC vuông góc với AO là theo tính chất hai tiếp tuyến đi qua 1 điểm A
b) Xét hai tam giác DCO và DBA có góc D chung và góc C = góc B = 90 độ (tính chất tiếp tuyến)
=> tam giác DCO đồng dạng với tam giác DBA
=> DC/DB = DO/DA
=> DC.DA = DO.DB (đpcm)
c) Vì OM vuông góc với DB => OM // BA (cùng vuông góc với DB)
Ta có AM/DM + 1 = (AM + DM)/DM = DA/DM
Theo Viet ta có: DA/DM = AB/MO
=> AM/DM + 1 = AB/OM
=> AB/OM - AM/DM = 1 (*)
Ta lại có tam giác MOA cân (vì góc MOA = góc BAO do so le trong, góc MAO = góc BAO do tính chất hai tiếp tuyến cùng 1 điểm)
=> OM = AM
(*) trở thành: AB/AM - AM/DM = 1 (đpcm)

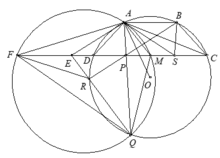
1). Gọi S điểm đối xứng với P qua M.Theo tính chất đối xứng của hình thang cân dễ thấy tứ giác ABSP cũng là hình thang cân.
Ta lại có Q P S ^ = Q A B ^ = Q R B ^ .
Từ đó có E P Q ^ = E R P ^ ⇒ Δ E R P ∽ Δ E P Q (g – g),
nên E Q P ^ = E P R ^ = B P S ^ = A S E ^ , suy ra tứ giác AEQS nội tiếp.
Do đó P A . P Q = P E . P S = P F 2 .2 P M = P F . P M , suy ra tứ giác A M Q F nội tiếp.
Từ đó suy ra đường tròn ngoại tiếp tam giác △ A Q F luôn đi qua M.
Cho tam giác ABC có 3 góc nhọn(AB<AC) nội tiếp đường tròn (O;R).Vẽ đường kính AD,tiếp tuyến với đường tròn (O;R) tại D cắt BC tại E.Vẽ OH vuông góc với BC (H #Hỏi cộng đồng OLM #Toán lớp 10


1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.