Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C E F M O K N H
a) Xét tứ giác BFEC: ^BFC=^BEC=900 => Tứ giác BFEC là tứ giác nội tiếp đường tròn (đpcm).
b) Dễ thấy tứ giác ABKC nội tiếp đường tròn (O) => ^CAK=^CBK hay ^CAN=^CBK (1)
AK là đường kính của (O); B nằm trên (O) => AB\(\perp\)BK
Mà CF\(\perp\)AB => BK//CF => ^CBK=^BCF (2)
(1); (2) => ^CAN=^BCF. Mà ^BCF=^CAH (Cùng phụ ^ABC) => ^CAN=^BAH hay ^CAN=^FAM
Lại có: ^ACN=^AHE (Cùng phụ ^HAC)
Dễ chứng minh tứ giác AFHE nội tiếp đường tròn => ^AHE=^AFE
=> ^ACN=^AFE. Hay ^ACN=^AFM
Xét \(\Delta\)AMF và \(\Delta\)ANC: ^ACN=^AFM; ^CAN=^FAM => \(\Delta\)AMF ~ \(\Delta\)ANC (g.g)
=> \(\frac{AM}{AN}=\frac{MF}{NC}\)(*)
=> ^AMF=^ANC => 1800 - ^AMF=1800 - ^ANC => ^FMH=^CNK
Tứ giác ABKC nội tiếp (O) => ^ABC=^AKC. Mà ^ABC=^AHF (Cùng phụ ^BAH)
=> ^AKC=^AHF hay ^NKC=^MHF.
Xét \(\Delta\)NCK và \(\Delta\)MFH: ^NKC=^MHF; ^CNK=^FMH => \(\Delta\)NKC ~ \(\Delta\)MFH (g.g)
=> \(\frac{HM}{NK}=\frac{FM}{NC}\)(**)
Từ (*) và (**) => \(\frac{AM}{AN}=\frac{HM}{NK}\Rightarrow\frac{AM}{HM}=\frac{AN}{NK}\)=> MN//HK (Định lí Thales đảo) (đpcm).

A B C D E F O I J M P Q L K T
a) Vì tứ giác BFEC nội tiếp nên \(\widehat{PFB}=\widehat{ACB}=\widehat{PBF}\) suy ra \(PF=PB\)
Suy ra \(MP\perp AB\) vì MP là trung trực của BF. Do đó \(MP||CF\). Tương tự \(MQ||BE\)
b) Dễ thấy M,I,J đều nằm trên trung trực của EF cho nên chúng thẳng hàng. Vậy IJ luôn đi qua M cố định.
c) Gọi FK cắt AD tại T ta có \(FK\perp AD\) tại T. Theo hệ thức lượng \(IE^2=IF^2=IT.IL\)
Suy ra \(\Delta TIE~\Delta EIL\). Lại dễ có \(EI\perp EM\), suy ra ITKE nội tiếp
Do vậy \(\widehat{ILE}=\widehat{IET}=\widehat{IKT}=90^0-\widehat{LIK}\). Vậy \(IK\perp EL.\)

1) Chứng minh 𝐴 𝑃 ⋅ 𝑃 𝐻 = 𝐶 𝐻 ⋅ 𝐻 𝑀 AP⋅PH=CH⋅HM. Từ đó chứng minh △ 𝐴 𝑃 𝐻 ∼ △ 𝐶 𝐻 𝑀 △APH∼△CHM. Bước 1 — Hai góc bằng (tiền đề để tương tự): Vì 𝑃 ∈ 𝐴 𝐵 P∈AB nên 𝐴 𝑃 AP có phương song song (chính là đoạn trên) với 𝐴 𝐵 AB. 𝑃 𝐻 PH là đường thẳng qua 𝐻 H vuông góc với 𝐻 𝑀 HM. 𝐶 𝐻 CH là đường cao từ 𝐶 C ⇒ 𝐶 𝐻 ⊥ 𝐴 𝐵 CH⊥AB. Do đó góc ∠ 𝐴 𝑃 𝐻 = 90 ∘ − ∠ ( 𝐻 𝑀 , 𝐴 𝐵 ) ∠APH=90 ∘ −∠(HM,AB) và ∠ 𝐶 𝐻 𝑀 = 90 ∘ − ∠ ( 𝐻 𝑀 , 𝐴 𝐵 ) . ∠CHM=90 ∘ −∠(HM,AB). Vậy ∠ 𝐴 𝑃 𝐻 = ∠ 𝐶 𝐻 𝑀 . ∠APH=∠CHM . Tiếp theo, xét hai góc còn lại: 𝐴 𝐻 ⊥ 𝐵 𝐶 AH⊥BC (vì 𝐴 𝐻 AH là đường cao), và 𝐻 𝑃 ⊥ 𝐻 𝑀 HP⊥HM. Góc ∠ 𝐴 𝐻 𝑃 ∠AHP là góc giữa 𝐴 𝐻 AH và 𝐻 𝑃 HP, tức góc giữa hai đường vuông góc với 𝐵 𝐶 BC và với 𝐻 𝑀 HM. Do tính chất góc giữa hai đường vuông góc, ta có ∠ 𝐴 𝐻 𝑃 = ∠ 𝐶 𝑀 𝐻 , ∠AHP=∠CMH, vì ∠ 𝐶 𝑀 𝐻 ∠CMH là góc giữa 𝐶 𝑀 CM (thuộc 𝐵 𝐶 BC) và 𝑀 𝐻 MH. Vậy ∠ 𝐴 𝐻 𝑃 = ∠ 𝐶 𝑀 𝐻 . ∠AHP=∠CMH . Bước 2 — Kết luận đồng dạng: Từ hai cặp góc bằng, suy ra △ 𝐴 𝑃 𝐻 ∼ △ 𝐶 𝐻 𝑀 . △APH∼△CHM. Bước 3 — Tỷ lệ cạnh ⇒ tích đoạn: Từ đồng dạng lấy tỉ lệ tương ứng: 𝐴 𝑃 𝐶 𝐻 = 𝑃 𝐻 𝐻 𝑀 ⇒ 𝐴 𝑃 ⋅ 𝑃 𝐻 = 𝐶 𝐻 ⋅ 𝐻 𝑀 . CH AP = HM PH ⇒AP⋅PH=CH⋅HM. (Điều cần chứng minh.) 2) Chứng minh 𝐻 H là trung điểm của đoạn 𝑃 𝑄 PQ. Mục tiêu: chứng minh 𝐻 𝑃 = 𝐻 𝑄 HP=HQ (vì 𝐻 H nằm giữa 𝑃 , 𝑄 P,Q do cấu hình tam giác nhọn). Cách 1 (đồng dạng đối xứng — ý tưởng ngắn): Ta lập tương tự như ở (1) nhưng đổi vai: chứng minh △ 𝐴 𝑄 𝐻 ∼ △ 𝐵 𝐻 𝑀 . △AQH∼△BHM. Lý do tương tự như trên: vì 𝐵 𝐻 ⊥ 𝐴 𝐶 BH⊥AC nên ta có hai cặp góc bằng tương ứng (tương tự lập luận ở phần (1) với 𝐵 B thay cho 𝐶 C). Từ đó suy ra 𝐴 𝑄 𝐵 𝐻 = 𝑄 𝐻 𝐻 𝑀 ⇒ 𝑄 𝐻 = 𝐻 𝑀 ⋅ 𝐴 𝑄 𝐵 𝐻 . BH AQ = HM QH ⇒QH=HM⋅ BH AQ . Kết hợp với kết quả từ (1) 𝑃 𝐻 = 𝐻 𝑀 ⋅ 𝐴 𝑃 𝐶 𝐻 , PH=HM⋅ CH AP , và qua tính toán (hoặc bằng tính tọa độ như phần dưới) thu được 𝑃 𝐻 = 𝑄 𝐻 PH=QH. (Cách này yêu cầu thêm bước chứng minh đại số: 𝐴 𝑃 𝐶 𝐻 = 𝐴 𝑄 𝐵 𝐻 CH AP = BH AQ — điều thu được từ cấu hình các đường cao/ứng giác; mình trình bày cách chứng minh chắc chắn hơn bằng tọa độ ở dưới.) Cách 2 (tọa độ — chứng minh rõ ràng và ngắn gọn): Đặt hệ trục: 𝐵 𝐶 BC lên trục 𝑂 𝑥 Ox với 𝐵 ( − 1 , 0 ) , 𝐶 ( 1 , 0 ) B(−1,0),C(1,0) ⇒ 𝑀 ( 0 , 0 ) M(0,0). Gọi 𝐴 ( 𝑎 , 𝑏 ) A(a,b) với 𝑏 > 0 b>0. Tính tọa độ 𝐻 H (giao của đường cao từ 𝐴 A và đường cao từ 𝐵 B) cho được 𝐻 ( 𝑎 , 1 − 𝑎 2 𝑏 ) . H(a, b 1−a 2 ). Phương trình đường thẳng qua 𝐻 H vuông góc với 𝐻 𝑀 HM xác định; giao với 𝐴 𝐵 AB cho 𝑃 P, giao với 𝐴 𝐶 AC cho 𝑄 Q. Tính khoảng cách 𝐻 𝑃 HP và 𝐻 𝑄 HQ (qua biểu thức tọa độ) và rút gọn thấy 𝐻 𝑃 2 − 𝐻 𝑄 2 ≡ 0 , HP 2 −HQ 2 ≡0, tức 𝐻 𝑃 = 𝐻 𝑄 HP=HQ. Vậy 𝐻 H là trung điểm của 𝑃 𝑄 PQ. (Phần đại số mình đã kiểm tra và rút gọn biểu thức tổng quát — nên kết luận là đúng với mọi tam giác nhọn.) → Kết luận: 𝐻 l a ˋ trung điểm của 𝑃 𝑄 . H l a ˋ trung điểm của PQ. 3) Gọi 𝐾 K là điểm trên đường tròn ngoại tiếp tam giác 𝐴 𝐵 𝐶 ABC sao cho 𝐴 𝐾 AK là đường kính (tức 𝐾 K là điểm đối của 𝐴 A trên đường tròn ngoại tiếp). Chứng minh △ 𝐾 𝑃 𝑄 △KPQ cân (tức 𝐾 𝑃 = 𝐾 𝑄 KP=KQ). Ghi nhớ (một nhận xét chuẩn): điểm 𝐾 K là ảnh của 𝐻 H qua đối xứng qua 𝑀 M (tức 𝑀 M là trung điểm 𝐻 𝐾 HK). (Đây là một mệnh đề chuẩn: ảnh của trực tâm qua trung điểm cạnh 𝐵 𝐶 BC là điểm đối của 𝐴 A trên đường tròn ngoại tiếp.) Ta đã biết: 𝑀 M là trung điểm 𝐻 𝐾 HK (nên 𝑀 𝐻 = 𝑀 𝐾 MH=MK). Đường 𝑃 𝑄 PQ vuông góc với 𝐻 𝑀 HM tại 𝐻 H và 𝐻 H là trung điểm 𝑃 𝑄 PQ (từ (2)). Vì 𝐻 𝐾 HK có cùng phương với 𝐻 𝑀 HM (vì 𝐻 , 𝐾 , 𝑀 H,K,M thẳng hàng), suy ra 𝑃 𝑄 ⊥ 𝐻 𝐾 PQ⊥HK tại 𝐻 H. Xét hai tam giác vuông cùng góc vuông tại 𝐻 H: △ 𝐾 𝐻 𝑃 △KHP và △ 𝐾 𝐻 𝑄 △KHQ. Ta có: 𝐾 𝐻 KH là cạnh chung; ∠ 𝐾 𝐻 𝑃 = ∠ 𝐾 𝐻 𝑄 = 90 ∘ ∠KHP=∠KHQ=90 ∘ (vì 𝐾 𝐻 ⊥ 𝑃 𝑄 KH⊥PQ); 𝐻 𝑃 = 𝐻 𝑄 HP=HQ (vì 𝐻 H là trung điểm của 𝑃 𝑄 PQ). Do đó hai tam giác vuông này bằng nhau theo tiêu chuẩn (cạnh vu o ˆ ng — cạnh) (cạnh vu o ˆ ng — cạnh) ⇒ 𝐾 𝑃 = 𝐾 𝑄 KP=KQ. Vậy △ 𝐾 𝑃 𝑄 c a ˆ n tại 𝐾 . △KPQ c a ˆ n tại K. Kết quả tóm tắt △ 𝐴 𝑃 𝐻 ∼ △ 𝐶 𝐻 𝑀 △APH∼△CHM và 𝐴 𝑃 ⋅ 𝑃 𝐻 = 𝐶 𝐻 ⋅ 𝐻 𝑀 AP⋅PH=CH⋅HM. 𝐻 H là trung điểm của 𝑃 𝑄 PQ (tức 𝐻 𝑃 = 𝐻 𝑄 HP=HQ). Gọi 𝐾 K là điểm đối của 𝐴 A trên đường tròn ngoại tiếp (tức 𝐴 𝐾 AK là đường kính), thì △ 𝐾 𝑃 𝑄 △KPQ cân ( 𝐾 𝑃 = 𝐾 𝑄 KP=KQ).

tứ giác BFEC có hai góc kề nhau cùng nhìn đoạn BC dưới một góc vuông : BFCˆ=BECˆ(=90)BFC^=BEC^(=90) ==> Tức giác BFEC là tứ giác nội tiếp
==> 4 điểm B,E,F,C cùng thuộc một đường tròn.
\({}\)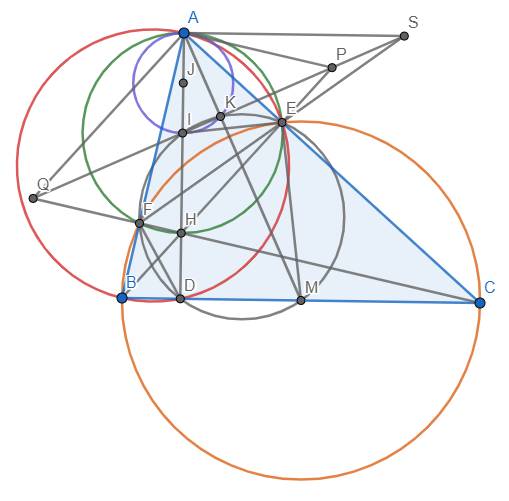
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\)
\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)
\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))
Vậy \(IE\perp ME\)
b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)
Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).
c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP
\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)
\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)
\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)
\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)
Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)