K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NN
25 tháng 3 2020
b) Vì AC=2AB
AB=BD
=>AC=AD
Xét tam giác ACE và tam giác ADE có:
AC=AD ( chứng minh trên )
^CAE=^EAD ( tính chất phân giác )
AE chung
=> tam giác ACE = tam giác ADE ( c.g.c )
=> ^CEA=^AED ( 2 góc tương ứng )
Mà ^CEA kề bù ^AED
=> ^CEA=^AED=90°
=> AE vuông góc CD
AI và AE là 2 tia trùng nhau
=> AI vuông góc CD
Vì AI vuông góc BM
Mà AI vuông góc CD
<=> BM // CD
Chúc bạn học tốt!
NN
25 tháng 3 2020
Vì mình không tìm được cách gõ góc nên kí hiệu ^ là góc nhé! Mong bạn thông cảm


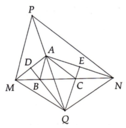

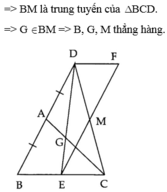

a: Xét ΔABC có
BM,CN là các đường trung tuyến
BM cắt CN tại G
Do đó: G là trọng tâm của ΔABC
=>\(BG=\dfrac{2}{3}BM=\dfrac{2}{3}\cdot15=10\left(cm\right)\)
b: Xét ΔABM và ΔCEM có
MA=MC
\(\widehat{AMB}=\widehat{CME}\)(hai góc đối đỉnh)
MB=ME
Do đó: ΔMAB=ΔMCE
=>\(\widehat{MAB}=\widehat{MCE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BA//CE
d: Xét ΔNBF và ΔNAC có
\(\widehat{NBF}=\widehat{NAC}\)(BF//AC)
NB=NA
\(\widehat{BNF}=\widehat{ANC}\)(hai góc đối đỉnh)
Do đó: ΔNBF=ΔNAC
=>NF=NC
Xét ΔNAF và ΔNBC có
NA=NB
\(\widehat{ANF}=\widehat{BNC}\)(hai góc đối đỉnh)
NF=NC
Do đó: ΔNAF=ΔNBC
=>AF=BC
ΔNAF=ΔNBC
=>\(\widehat{NAF}=\widehat{NBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//BC
Xét ΔMAE và ΔMCB có
MA=MC
\(\widehat{AME}=\widehat{CMB}\)(hai góc đối đỉnh)
ME=MB
Do đó: ΔMAE=ΔMCB
=>AE=CB
ΔMAE=ΔMCB
=>\(\widehat{MAE}=\widehat{MCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
Ta có: AE//BC
AF//BC
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
mà AE=AF(=BC)
nên A là trung điểm của EF